
【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
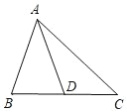
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
【答案】(1)详见解析;(2)A'B=AC;(3)AB+AC>2AD,理由详见解析.
【解析】
(1)作图;
(2)证明△ADC≌△A'DB,可知AC=A'B;
(3)根据三角形三边关系得:AB+BA'>AA',即AB+AC>AD+A'D,所以AB+AC>2AD.
(1)如图所示,延长 AD 至 A',使 AD=A'D,连接 A'B,则△A'DB 就是与△ACD 关于点 D 成中心对称的三角形;

(2)A'B=AC,
理由是:在△ADC 和△A'DB 中,
∵ ,
,
∴△ADC≌△A'DB(SAS),
∴AC=A'B;
(3)AB+AC>2AD;
理由:∵△ADC 与△A'DB 关于 D 点成中心对称,
∴AD=A'D,AC=A'B.
在△ABA'中,AB+BA'>AA', 即 AB+AC>AD+A'D.
∴AB+AC>2AD.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
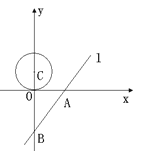
【题目】如图,已知直线![]() 的解析式是
的解析式是![]() ,并且与
,并且与![]() 轴、
轴、![]() 轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着
轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着![]() 轴向下运动,当⊙C与直线
轴向下运动,当⊙C与直线![]() 相切时,则该圆运动的时间为( )
相切时,则该圆运动的时间为( )
A. 3秒或6秒 B. 6秒 C. 3秒 D. 6秒或16秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0),B(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(提示:平行四边形的面积=底×高)
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
的值是否发生变化,若不变请求出该值,若会变请并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
,![]() (如图1).
(如图1).
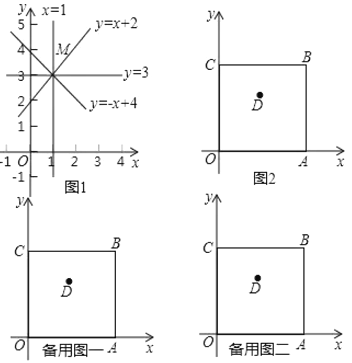
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)分解因式:
①x2-8xy+16y2
②(x+y+1)2-(x-y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )

A.BC = EFB.AC//DFC.∠C = ∠FD.∠BAC = ∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com