【题目】如图，∠A=15°，AB=BC=CD=DE=EF，则∠DEF等于（ ）
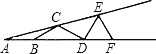
A．90° B．75° C．70° D．60°
【答案】D
【解析】
试题分析:根据已知条件，利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算．
解：∵AB=BC=CD=DE=EF，∠A=15°，
∴∠BCA=∠A=15°，
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°，
∴∠BCD=180°﹣（∠CBD+∠BDC）=180°﹣60°=120°，
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°，
∴∠CDE=180°﹣（∠ECD+∠CED）=180°﹣90°=90°，
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°，
∴∠DEF=180°﹣（∠EDF+∠EFC）=180°﹣120°=60°．
故选D．
科目：初中数学 来源： 题型：
【题目】2016年2月上旬福州地区空气质量指数（AQI）如下表所示，空气质量指数不大于100表示空气质量优良，如果小王该月上旬来福州度假三天那么他在福州度假期间空气质量都是优良的概率是 .
2016年2月上旬福州地区空气质量指数（AQI）
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ug/m3 | 26 | 34 | 43 | 41 | 34 | 48 | 78 | 1 15 | 59 | 45 |
查看答案和解析>>
科目：初中数学 来源： 题型：
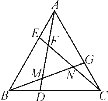
【题目】如图，已知△ABC是等边三角形，E，D，G分别在AB，BC，AC边上，且AE＝BD＝CG.连接AD，BG，CE，相交于F，M，N.
(1)求证：AD＝CE；
(2)求∠DFC的度数；
(3)试判断△FMN的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
（1）2n﹣（2﹣n）+（6n﹣2），其中n=﹣2；
（2）﹣（3a2﹣4ab）+[a2﹣2（2a+2ab）]，其中a=﹣2，b= 
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠A=30°，AB=AC，以B为圆心，BC长为半径画弧，交AC于点D，交AB于点E.
（1）求∠ABD的度数；
（2）当BC=
时，求线段AE，AD与
围成阴影部分的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
