
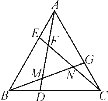
【题目】如图,已知△ABC是等边三角形,E,D,G分别在AB,BC,AC边上,且AE=BD=CG.连接AD,BG,CE,相交于F,M,N.
(1)求证:AD=CE;
(2)求∠DFC的度数;
(3)试判断△FMN的形状,并说明理由.
【答案】(1)见解析;(2)60°;(3)等边三角形,理由见解析.
【解析】试题分析:(1)求证ABDCAE即可证明AD=CE;(2)由三角形外角的性质可以得到∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°;(3)与(2)同样的道理可证∠FMN=∠FNM=∠DFC=60°,即可证得△FMN是等边三角形。
解:(1)证明:∵△ABC是等边三角形,
∴∠BAC=∠ABC=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE.
(2)由(1)知△AEC≌△BDA,
∴∠ACE=∠BAD.
∴∠DFC=∠FAC+∠ACE=∠FAC+∠BAD=60°.
(3)△FMN为等边三角形,由(2)知∠DFC=60°,
同理可求得∠AMG=60°,∠BNF=60°.
∴△FMN是等边三角形.


科目:初中数学 来源: 题型:
【题目】义务教育均衡发展是一种新的教育发展观,是解决我国目前教育问题的新举措.其最终目标,就是要合理配置教育资源,办好每一所学校,教好每一个学生,实现教育公平.我们县级政府为推进义务教育均衡发展工作的评估,今年预算办学经费约为3亿5千万,请你用科学记数法表示应是( )
A.3.5×108
B.3.5×109
C.35×108
D.0.35×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条信息在一周内被转发了2180000次,将数据2180000用科学记数法表示为( )
A. 2.18×105 B. 2.18×106 C. 21.8×106 D. 21.8×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的进价为 300 元,售价为 550 元.后来由于该商品积压,商店准备打折销售, 但要保证利润率为 10%,则该商品可打_____折.
查看答案和解析>>
科目:初中数学 来源: 题型:
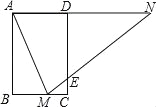
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
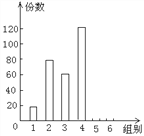
【题目】某报社在国庆前夕开展了随报有奖竞赛活动,限于9月1日到9月30日上交答卷,编辑部把学生上交的答卷份数按5天一组分组统计,绘制了如图所示的条形统计图.已知从左到右各长方形的高的比为1:4:3:6.第3组的答卷份数为60,第5、6组的答卷份数分别为80和40.
(1)补上第5、6组的条形图;
(2)本次活动共有多少份答卷?
(3)第几组上交答卷的份数最多?有多少份?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC经过平移后,使点A与点A′(﹣1,4)重合.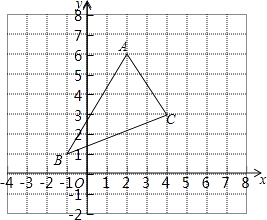
(1)画出平移后的△A′B′C′;
(2)求出△A′B′C′的面积;
(3)若三角形ABC内有一点P(a,b),经过平移后的对应点P′的坐标;
(4)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com