
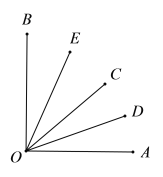
【题目】如图,![]() 是直角,射线
是直角,射线![]() 在
在![]() 的内部,
的内部,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)![]() 的度数是否随着射线
的度数是否随着射线![]() 的位置变化而变化?如果不变,请说明理由;如果变化,请说明是如何变化的.
的位置变化而变化?如果不变,请说明理由;如果变化,请说明是如何变化的.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不变,理由见解析.
;(3)不变,理由见解析.
【解析】
(1)根据直角的定义可求出∠BOC的度数,根据角平分线的定义可求出∠COE和∠COD的度数,进而可得∠DOE的度数;
(2)根据直角的定义可求出∠BOC的度数,根据角平分线的定义可求出∠COE和∠COD的度数,进而可得∠DOE的度数;
(3)根据角平分线的定义可得∠COE=![]() ∠BOC,∠DOC=
∠BOC,∠DOC=![]() ∠AOC,即可得∠DOE=
∠AOC,即可得∠DOE=![]() ∠AOB,即可得∠DOE的度数不变.
∠AOB,即可得∠DOE的度数不变.
(1)∵∠AOC=30°,∠AOB是直角,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,![]() 是直角,
是直角,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)不变,理由如下:
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
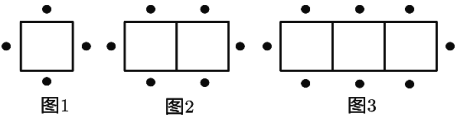
【题目】一张正方形桌子可坐4人,按图1—图3的方式将桌子拼在一起并安排人员就坐.
(1)两张桌子拼在一起可做 人,三张桌子拼在一起可坐 人,![]() 张桌子拼在一起可坐 人
张桌子拼在一起可坐 人
(2)一家酒楼有60张这样的桌子,按照图1—图3方式每4张拼成一个大桌子,则60张桌子可拼成15张大桌子,共可坐 人
(3)在问题(2)中,若每4张桌子拼成一个大的正方形桌子,则可坐 人
查看答案和解析>>
科目:初中数学 来源: 题型:
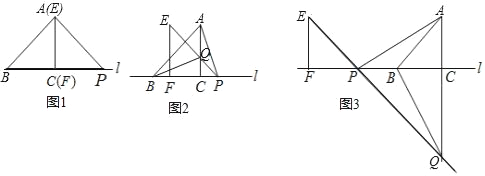
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k>0)的图象与一次函数y=
(k>0)的图象与一次函数y=![]() x的图象交于A、B两点(点A在第一象限).
x的图象交于A、B两点(点A在第一象限).

(1)当点A的横坐标为4时.
①求k的值;
②根据反比例函数的图象,直接写出当﹣4<x<2(x≠0)时,y的取值范围;
(2)点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
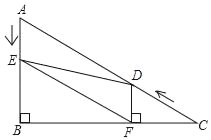
【题目】如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
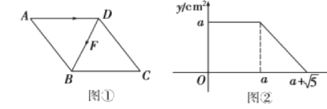
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 称为第 1 个三角形,它的周长是 1,以它的三边中点为顶点组成第 2 个三角形,再以第 2 个三角形的三边中点为顶点组成第 3 个三角形,以此类推,则第 2019 个三角形的周长为( )
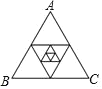
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,市里组织了一次“汉字听写”大赛,我区有1200名初三学生参加区级初赛,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(满分50分),整理得到如下的统计图表:

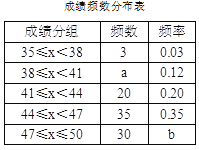
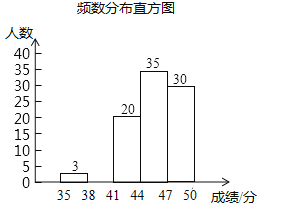
请根据所提供的信息解答下列问题:
(1)样本的中位数是________分;
(2)若按成绩分组情况绘制成扇形统计图,则表示47≤x≤50这组的扇形圆心角为_______°;
(3)请补全频数分布直方图;
(4)请根据抽样统计结果,估计我区初赛中成绩不低于41分的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com