
【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,
四个结论中成立的是( )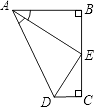
A.①②④
B.①②③
C.②③④
D.①③
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( ) 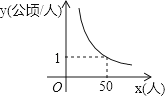
A.该村人均耕地面积随总人口的增多而增多
B.该村人均耕地面积y与总人口x成正比例
C.若该村人均耕地面积为2公顷,则总人口有100人
D.当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°. 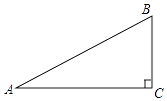
(1)用尺规在AC边上求作点D,使AD=BD;(保留痕迹,不写作法)
(2)若(1)中所得BD平分∠ABC,则∠A= . (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中:①全班学生家庭一周内收看“新闻联播”的次数;②某品牌灯泡的使用寿命;③长江中现有鱼的种类;④对乘坐民用航班的人员是否带有违禁物品的检查.期中适合抽样调查的是______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
﹣ 5,﹣2.626 626 662…,0,π,﹣ ![]() ,0.12,|﹣6|.
,0.12,|﹣6|.
(1)正数集合:{}
(2)负数集合:{}
(3)有理数集合:{};
(4)无理数集合:{}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是双曲线![]() 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线![]() 上运动,则k的值是 .
上运动,则k的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D.得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;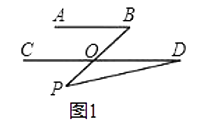
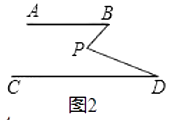
(2)在如图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明);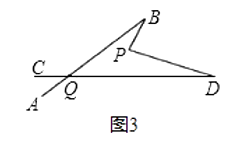
(3)根据(2)的结论求如图4中∠A+∠B+∠C+∠D+∠E的度数.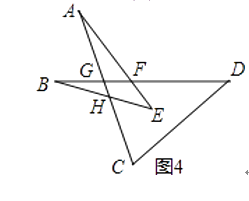
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中正确的是( )
A.对角线互相垂直的四边形是菱形
B.三个角相等的四边形是矩形
C.对角线相等的平行四边形是正方形
D.对角线互相平分垂直且相等的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com