
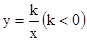 的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-
的图像上一点,过D作DE⊥x轴于E, DC⊥y轴于C,一次函数y=-x+m与y=-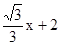 的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.
的图象都经过点C,与x轴分别交于A、B两点,四边形DCAE的面积为4,求k的值.科目:初中数学 来源:不详 题型:解答题
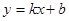 的图象与反比例函数
的图象与反比例函数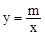 的图象交于A、B两点。
的图象交于A、B两点。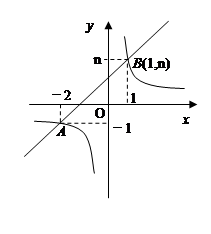
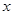 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
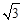 ,3),AB⊥x轴于B,连接OA,反比例函数
,3),AB⊥x轴于B,连接OA,反比例函数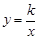 (k >0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的
(k >0)的图象与线段OA、AB分别交于点C、D.若AB=3BD,以点C为圆心,CA的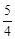 倍的长为半径作圆,则该圆与x轴的位置关系是 .(填“相离”、“相切”或“相交”).
倍的长为半径作圆,则该圆与x轴的位置关系是 .(填“相离”、“相切”或“相交”).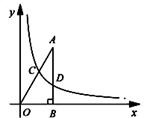
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
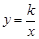 的图象经过(1,-2).
的图象经过(1,-2).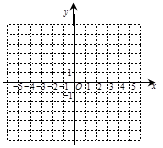
|
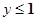 时,
时,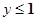 时,x的取值范围;当
时,x的取值范围;当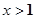 时,y的取值范围.
时,y的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
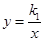 和
和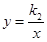 (
(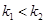 )在第一象限的图象,直线
)在第一象限的图象,直线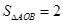 ,则
,则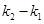 的值是 ( )
的值是 ( )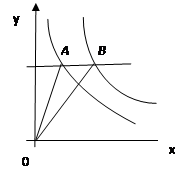
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
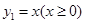 ,
, 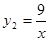
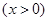 的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当
的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当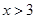 时,
时,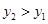 ③ 当
③ 当 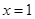 时, BC = 8 ④当
时, BC = 8 ④当 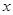 逐渐增大时,
逐渐增大时,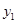 随着
随着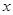 的增大而增大,
的增大而增大,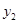 随着
随着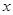 的增大而减小.其中正确结论的序号是 .
的增大而减小.其中正确结论的序号是 .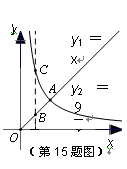
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
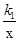 和y=
和y= 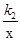 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )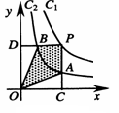
| A.k1+k2 | B.k1-k2 | C.k1·k2 | D.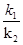 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com