
【题目】如图,长方形ABOD的顶点A是函数y=-x-(k+1)的图象与函数y=![]() 在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C的坐标;
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.

【答案】(1)反比例函数的表达式为y=-![]() ,一次函数的表达式为y=-x+2(2)点A,C的坐标分别为(-1,3),(3,-1)(3)点P的坐标为(0,
,一次函数的表达式为y=-x+2(2)点A,C的坐标分别为(-1,3),(3,-1)(3)点P的坐标为(0, ![]() )或(0,-
)或(0,-![]() )
)
【解析】试题分析:(1)根据图象所在的象限结合矩形ABOD的面积,就能求出k的值,进而求出两函数的表达式;
(2)将两函数解析式联立消元,求出其解,即得到交点A、C的坐标;
(3),设点P的坐标为(0,m),直线y=-x+2与y轴的交点坐标为M(0,2),根据S△APC=S△AMP+S△CMP=5解答即可.
试题解析:(1)由图象知k<0,由已知条件得|k|=3,
∴k=-3.
∴反比例函数的表达式为y=-![]() ,
,
一次函数的表达式为y=-x+2.
(2)由y=-![]() 与y=-x+2可得,-
与y=-x+2可得,- ![]() =-x+2,
=-x+2,
去分母整理后得x2-2x-3=0,
x2-2x+1-4=0,
(x-1)2=4,
∴x-1=±2,
即x1=-1,x2=3.
∴y1=3,y2=-1.
∴点A,C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),直线y=-x+2与y轴的交点为M,则M的坐标为(0,2).
∵S△APC=S△AMP+S△CMP=![]() ×PM×(|-1|+|3|)=5,
×PM×(|-1|+|3|)=5,
∴PM=![]() ,即|m-2|=
,即|m-2|=![]() .
.
∴m=![]() 或m=-
或m=-![]() .
.
∴点P的坐标为(0, ![]() )或(0,-
)或(0,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】在我市开展“阳光”活动中,为解中学生活动开展情况,随机抽查全市八年级部分同学1分钟,将抽查结果进行,并绘制两个不完整图.请根据图中提供信息,解答问题:
(1)本次共抽查多少名学生?
(2)请补全直方图空缺部分,直接写扇形图中范围135≤x<155所在扇形圆心角度数.
(3)若本次抽查中,在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生成绩为优秀?
(4)请你根据以上信息,对我市开展学生活动谈谈自己看法或建议
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店计划购进甲、乙两种新型汽车共140辆,这两种汽车的进价、售价如下表:
进价(万元/辆) | 售价(万元/辆) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)若该汽车专卖店投入1000万元资金进货,则购进甲乙两种新型汽车各多少辆?
(2)若该汽车专卖店准备乙种型号汽车的进货量不超过甲种型号汽车的进货量的3倍,应怎样安排进货方案,才能使该汽车专卖店售完这两种新型汽车后获得的利润最大?最大利润是多少?(其它成本不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边分别为a,b,c,△A'B'C'的三边分别为a',b',c',且有a2+a'2+b2+b'2+c2+c'2=2ab'+2bc'+2ca',则△ABC与△A'B'C'( )
A. 一定全等 B. 不一定全等 C. 一定不全等 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
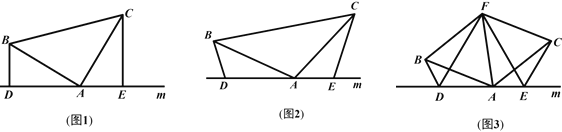
【题目】(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?若成立,请给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点
互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( ).

A.2![]() B.4
B.4![]() C.4 D.8
C.4 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com