
【题目】如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为 ![]() 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 .
的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为cm2 . 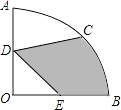
【答案】( ![]() π+
π+ ![]() ﹣
﹣ ![]() )
)
【解析】解:连结OC,过C点作CF⊥OA于F, 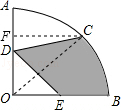
∵半径OA=2cm,C为 ![]() 的中点,D、E分别是OA、OB的中点,
的中点,D、E分别是OA、OB的中点,
∴OD=OE=1cm,OC=2cm,∠AOC=45°,
∴CF= ![]() ,
,
∴空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积
= ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() π﹣
π﹣ ![]() (cm2)
(cm2)
三角形ODE的面积= ![]() OD×OE=
OD×OE= ![]() (cm2),
(cm2),
∴图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积
= ![]() ﹣(
﹣( ![]() π﹣
π﹣ ![]() )﹣
)﹣ ![]()
= ![]() π+
π+ ![]() ﹣
﹣ ![]() (cm2).
(cm2).
故图中阴影部分的面积为( ![]() π+
π+ ![]() ﹣
﹣ ![]() )cm2 .
)cm2 .
故答案为:( ![]() π+
π+ ![]() ﹣
﹣ ![]() ).
).
连结OC,过C点作CF⊥OA于F,先根据空白图形ACD的面积=扇形OAC的面积﹣三角形OCD的面积,求得空白图形ACD的面积,再根据三角形面积公式得到三角形ODE的面积,再根据图中阴影部分的面积=扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积,列式计算即可求解.


科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图: 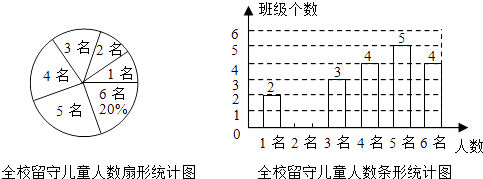
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )

A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 骑车的同学从出发到追上步行的同学用了20分钟
D. 步行的速度是6千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,作射线
边的中点,作射线![]() ,与边
,与边![]() 交于点
交于点![]() ,射线
,射线![]() 与直线
与直线![]() 交于点
交于点![]() ,且满足
,且满足![]() .
.
(![]() )如图
)如图![]() ,求证:
,求证: ![]() .
.
(![]() )在点
)在点![]() 运动的过程中,直接写出
运动的过程中,直接写出![]() ,
, ![]() ,
, ![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形 ABCDE 中,∠A+∠B+∠E=α,DP,CP 分别平分∠EDC,∠BCD,则∠P 的度数是( )

A. 90°+![]() α B.
α B. ![]() α﹣90° C.
α﹣90° C. ![]() α D. 540° -
α D. 540° -![]() α
α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.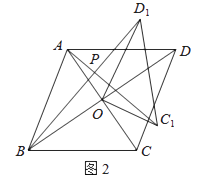
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.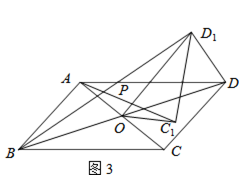
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.( ![]() 取1.73)
取1.73) 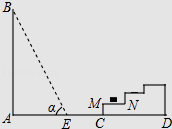
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点, ![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() 函数
函数![]() 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
![]() 连接CO,求证:
连接CO,求证: ![]() ;
;
![]() 若
若![]() 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标;
![]() 当直线PO与
当直线PO与![]() 相切时,求
相切时,求![]() 的度数;当直线PO与
的度数;当直线PO与![]() 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令![]() ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com