
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.( ![]() 取1.73)
取1.73) 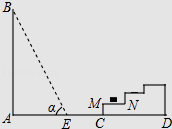
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
【答案】
(1)解:当α=60°时,在Rt△ABE中,
∵tan60°= ![]() =
= ![]() ,
,
∴AB=10tan60°=10 ![]() ≈10×1.73=17.3米.
≈10×1.73=17.3米.
即楼房的高度约为17.3米;
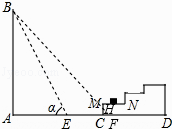
(2)解:当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan45°= ![]() =1,
=1,
此时的影长AF=AB=17.3米,
∴CF=AF﹣AC=17.3﹣17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
【解析】(1)在Rt△ABE中,由tan60°= ![]() =
= ![]() ,即可求出AB=10tan60°=17.3米;(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
,即可求出AB=10tan60°=17.3米;(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.


科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一条直线与反比例函数y= ![]() (x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y=
(x>0)的图象交于两点A、B,与x轴交于点C,且点B是AC的中点,分别过两点A、B作x轴的平行线,与反比例函数y= ![]() (x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( )
(x>0)的图象交于两点D、E,连接DE,则四边形ABED的面积为( ) 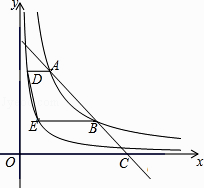
A.4
B.![]()
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形. 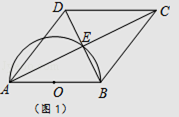
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连结OE,求△OBE的面积.
②求扇形AOE的面积.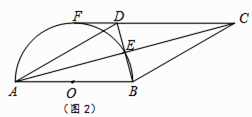
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算(2a+1)2﹣(2a+1)(﹣1+2a);
(2)用乘法公式计算:20022﹣2001×2003;
(3)解不等式组: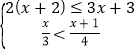 ,并把解集在数轴上表示出来;
,并把解集在数轴上表示出来;
(4)解方程组: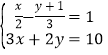 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作实践:△ABC中,∠A=90°,∠B=22.5°,请画出一条直线把△ABC分割成两个等腰三角形,并标出分割成两个等腰三角形底角的度数;(要求用两种不同的分割方法)
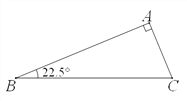
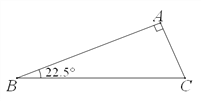
(2)分类探究:△ABC中,最小内角∠B=24°,若△ABC被一直线分割成两个等腰三角形,请画出相应示意图并写出△ABC最大内角的所有可能值;
(3)猜想发现:若一个三角形能被一直线分割成两个等腰三角形,需满足什么条件?(请你至少写出两个条件,无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了支援灾区学校灾后重建,我校决定再次向灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆,将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套, 一辆乙货车可装床
架10个和课桌凳10套.
(1)学校安排甲、乙两种货车可一次性把这些物资运到灾区有哪几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费
最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com