
【题目】为了支援灾区学校灾后重建,我校决定再次向灾区捐助床架60个,课桌凳100套.现计划租甲、乙两种货车共8辆,将这些物质运往灾区,已知一辆甲货车可装床架5个和课桌凳20套, 一辆乙货车可装床
架10个和课桌凳10套.
(1)学校安排甲、乙两种货车可一次性把这些物资运到灾区有哪几种方案?
(2)若甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,则学校应选择哪种方案,使运输费
最少?最少运费是多少?
【答案】(1)有3种方案,见解析;(2)8400元.
【解析】(1)设可租用甲种货车x辆,乙种货车辆,因为要一次性运送,所以所装的货物应该不少已60个床架和100套桌椅,根据题目所给的其他条件可列出不等式组.
(2)因为甲种货车每辆须付运费1200元,乙种货车要付1000元,所以乙种货车越多越省钱.选择方案可算出费用.
(1)设学校租甲种货车x辆,则租乙种货车(8-x)辆,
依题意,得 ![]() ,
,
解不等式组,得![]() ,
,
∵x为正整数,
∴ x的值为2,3,4.
∴学校安排甲、乙两种货车可一次性把这些物资运到灾区有3种方案:
方案1:租甲种货车2辆,租乙种货车6辆;
方案2:租甲种货车3辆,租乙种货车5辆;
方案3:租甲种货车4辆,租乙种货车4辆.
(2)因为甲种货车每辆要付运输费1200元,乙种货车要付运输费1000元,
且甲、乙两种货车共租8辆,所以租甲种货车越少,运输费越少.
所以方案1:租甲种货车2辆,租乙种货车6辆运输费最少,
此时运输费为1200×2+1000×6=8400(元).


科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.( ![]() 取1.73)
取1.73) 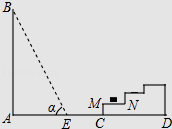
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点, ![]() 的圆心坐标为
的圆心坐标为![]() ,半径为
,半径为![]() 函数
函数![]() 的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点.
![]() 连接CO,求证:
连接CO,求证: ![]() ;
;
![]() 若
若![]() 是等腰三角形,求点P的坐标;
是等腰三角形,求点P的坐标;
![]() 当直线PO与
当直线PO与![]() 相切时,求
相切时,求![]() 的度数;当直线PO与
的度数;当直线PO与![]() 相交时,设交点为E、F,点M为线段EF的中点,令
相交时,设交点为E、F,点M为线段EF的中点,令![]() ,求s与t之间的函数关系,并写出t的取值范围.
,求s与t之间的函数关系,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“五一劳动节”,某超市开展促销活动,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要108元,买3件A商品和4件B商品需要94元.问:打折后,若买5件A商品和4件B商品仅需86元,比打折前节省了多少元钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 ![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
A.(-3,0)
B.(-2,0)
C.x=-3
D.x=-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1 , x2满足x1+x2=4和x1x2=3,那么二次函数ax2+bx+c(a>0)的图象有可能是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知a,b满足![]() ,解关于x的方程(a+2)x+b2=a-1.
,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为![]() ,求代数式x2+(a+b)cdx+
,求代数式x2+(a+b)cdx+![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com