
����Ŀ��ijѧϰ��ȤС��μ�һ�ε�Ԫ���飬�ɼ�ͳ��������±���

(1)��ȤС�鱾�ε�Ԫ���Գɼ���ƽ��������λ�����������Ƕ��٣�
(2)��ʦ����Ϊ��ȤС���µ�Ԫ�����趨һ����Ŀ�꣬ѧ���ﵽ��Ŀ����轱������ϣ��С������֮һ���ҵ�����ѧ���õ��������������ʦ��ƽ��������λ����������������ѡ��һ���Ƚ�ǡ����Ŀ����������ƻ���һ�����ҵ��˶��õ�������ȷ���ĸ�����ΪĿ��ǡ��Щ��
���𰸡���1��ƽ������80.3�֣���λ����78�֣�������75�֣���2��ƽ��������λ��
��������
��1������ƽ��������λ���������Ķ�����⣻
��2�������������ƽ��������λ�����������з�����ɣ�
��1��ƽ����Ϊ��![]() ��73+74+75��5+76��4+77��3+78��2+79��3+82+83+84+86��2+88��3+90+92��2��=80.3���֣���
��73+74+75��5+76��4+77��3+78��2+79��3+82+83+84+86��2+88��3+90+92��2��=80.3���֣���
���մ�С�����˳�����У�����30������λ�ڵ�15����16��������78��������λ���ǣ�78+78����2=78���֣���
75������5�Σ�������࣬����������75�֣�
��2���ɣ�1����֪��ƽ����Ϊ80.3�֣���λ��Ϊ78�֣�����Ϊ75�֣�
���ϣ��С������֮һ���ҵ�����ѧ���õ���������ʦ����ѡ��ƽ������
����ƻ���һ�����ҵ��˶��õ�������������λ�����ϵ�����ռ��������һ�����ҿɵã�ȷ����λ����ΪĿ��ǡ��Щ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x��һԪ���η���x2����2m+3��x+m2+3m+2=0��
��1����֪x=2�Ƿ��̵�һ��������m��ֵ��
��2����������̵�����ʵ������Ϊ��ABC��AB��AC��AB��AC���ı߳�����BC=![]() ʱ����ABC�ǵ��������Σ����ʱm��ֵ.
ʱ����ABC�ǵ��������Σ����ʱm��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x��һԪ���η���x2����2m+3��x+m2+3m+2=0��
��1����֪x=2�Ƿ��̵�һ��������m��ֵ��
��2����������̵�����ʵ������Ϊ��ABC��AB��AC��AB��AC���ı߳�����BC=![]() ʱ����ABC�ǵ��������Σ����ʱm��ֵ.
ʱ����ABC�ǵ��������Σ����ʱm��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=90�㣬��BAC=60�㣬AC�Ƶ�C˳ʱ����ת60����CD��F��CD���е㣬����BF��AC�ڵ�E������AD��
��֤����1��AC=BF��
��2���ı���ABFD��ƽ���ı��Σ�
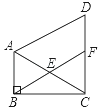
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y=![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���ȵõ�һ���µĺ��������Ա���xȡ1��2��3��4��5����������������ʱ���µĺ���ֵ�ֱ�Ϊy1��y2��y3��y4��y5������������Сֵ�����ֵ�ֱ�Ϊ��������
����λ���ȵõ�һ���µĺ��������Ա���xȡ1��2��3��4��5����������������ʱ���µĺ���ֵ�ֱ�Ϊy1��y2��y3��y4��y5������������Сֵ�����ֵ�ֱ�Ϊ��������
A. y1��y2 B. y43��y44 C. y44��y45 D. y2014��y2015
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��l��y=![]() x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=
x+m��x�ᡢy��ֱ��ڵ�A�͵�B��0����1����������y=![]() x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
x2+bx+c������B����ֱ��l����һ������ΪC��4��n����
��1����n��ֵ�������ߵĽ���ʽ��
��2����D���������ϣ�DE��y�ύֱ��l�ڵ�E����F��ֱ��l�ϣ����ı���DFEGΪ���Σ���ͼ2�������D�ĺ�����Ϊt��0��t��4��������DFEG���ܳ�Ϊp����p��t�ĺ�����ϵʽ�Լ�p�����ֵ��
��3������AOB��ƽ����ij��M��ת90���180�㣬�õ���A1O1B1����A��O��B�Ķ�Ӧ��ֱ��ǵ�A1��O1��B1������A1O1B1����������ǡ�������������ϣ���ô���Ǿͳ������ĵ�Ϊ����㡱����ֱ��д������㡱�ĸ�������ת180��ʱ��A1�ĺ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��![]() �ϰڷ�������������
�ϰڷ�������������
(1)��ͼ1����֪ˮƽ���õ����������εı߳�������![]() ��б�ŷ��õ������ε����
��б�ŷ��õ������ε����![]() _ ������ֱ�������ε����֮��Ϊ____ (����
_ ������ֱ�������ε����֮��Ϊ____ (����![]() ��ʾ)
��ʾ)

(2)��ͼ2��С���������![]() �� б�ŷ��õ������ε����
�� б�ŷ��õ������ε����![]() ����ͼ�������۽������ε����
����ͼ�������۽������ε����![]() _ ��
_ ��![]() _
_

(3)ͼ3�����������������ɵ�ƽ��ͼ��![]() ��
��![]() �ֱ��ʾ���ڵ��������������ε��������д��
�ֱ��ʾ���ڵ��������������ε��������д��![]() _ ��
_ ��![]() _ .(����
_ .(����![]() ��ʾ)
��ʾ)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������̵ĺ���������Σ���ˮ��AB���±�i=1��![]() ����AB=30m������ͬѧ�ڴ����A�㴦�ø�1.5m�IJ����Dz����ѹ���߸�CD����D������Ϊ30�㣬��֪����BC��30m�����ѹ���߸�CD�ĸ߶ȣ��������������Ч���֣�
����AB=30m������ͬѧ�ڴ����A�㴦�ø�1.5m�IJ����Dz����ѹ���߸�CD����D������Ϊ30�㣬��֪����BC��30m�����ѹ���߸�CD�ĸ߶ȣ��������������Ч���֣�![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һλ�˶�Ա�ھ�����4m������Ͷ���������е�·���������ߣ��������е�ˮƽ������2.5mʱ���ﵽ���߶�3.5m��Ȼ��ȷ������Ȧ����֪��Ȧ���ĵ�����ľ���Ϊ3.05m��
��1��������ͼ��ʾ��ƽ��ֱ������ϵ���������ߵĽ���ʽ��
��2�����˶�Ա����1.8m���������Ͷ�У�����ͷ����0.25m�����֣�
�ʣ������ʱ�����������ĸ߶��Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com