
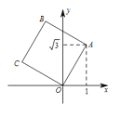
【题目】如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,![]() ),则点C的坐标( )
),则点C的坐标( )
A.(-1,![]() )B.(
)B.(![]() )C.
)C.![]() D.(-2,1)
D.(-2,1)
【答案】B
【解析】
作AD⊥轴于D,作CE⊥x轴于E,则∠ADO=∠OEC=90°,得出∠1+∠2=90°,由正方形的性质得出OC=AO,∠1+∠3=90°,证出∠3=∠2,由AAS证明△OCE≌△AOD,OE=AD=![]() ,CE=OD=1,即可得出结果.
,CE=OD=1,即可得出结果.
解:作AD⊥轴于D,作CE⊥x轴于E,如图所示:
则∠ADO=∠OEC=90°,
∴∠1+∠2=90°,
∵点A的坐标为(1,![]() ),
),
∴OD=1,AD=![]() ,
,
∵四边形OABC是正方形,
∴∠AOC=90°,OC=AO,
∴∠1+∠3=90°,
∴∠3=∠2,
在△OCE和△AOD中,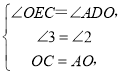 ,
,
∴△OCE≌△AOD(AAS),
∴OE=AD=![]() ,CE=OD=1,
,CE=OD=1,
∴点C的坐标为(-![]() ,1);
,1);
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.

(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan53°≈1.33, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做整数点,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
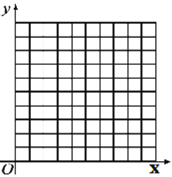
(1)填表:
点P从O点出发的时间 | 可以到达的整坐标 | 可以到达整数点的个数 |
1秒 | (0,1),(1,0) | 2 |
2秒 | (0,2),(2,0),(1,1) | 3 |
3秒 | ( ) | ( ) |
(2)当点P从点O出发10秒,可到达的整数点的个数是____________个;
(3)当点P从O点出发____________秒时,可得到整数点(10,5).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
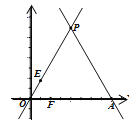
查看答案和解析>>
科目:初中数学 来源: 题型:
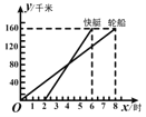
【题目】如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t(时)变化的图象,根据图象回答下列问题
(1)轮船的行驶速度是___________km/h;
(2)当2≤t≤6时,求快艇行驶过程y与t的函数关系式;
(3)当快艇与乙港相距40 km时,快艇和轮船相距___________km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请观察下列算式,找出规律并填空
![]() =1-
=1-![]() ,
, ![]() =
=![]() -
-![]() ,
, ![]() =
=![]() -
-![]() ,
, ![]() =
=![]() -
-![]()
则第10个算式是 _____________=_____________
第n个算式是 ___________=_____________
根据以上规律解答以下三题:(1)![]()
(2)若有理数a、b满足|a-1|+![]() =0 ,试求:
=0 ,试求:
![]() +
+![]() +
+![]() + …+
+ …+![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C三个点,请回答:

(1)如果将A点向右移动4个单位长度,表示什么数?
(2)如果将点C向左移动3个单位长度,三个点中哪个点表示的数最大?是多少?
(3)如果点A、点B同时向右运动,点A的速度是2个单位/秒,点B的速度是1个单位/秒,问经过多长时间两点重合?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com