
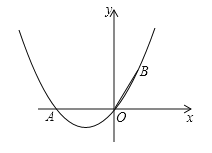
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)(-1,
;(2)(-1,![]() );(3) M1(-1,-
);(3) M1(-1,-![]() ),M2(-3,
),M2(-3,![]() ),M3(1,
),M3(1,![]() ).
).
【解析】
(1)先确定出点B坐标,再用待定系数法即可;
(2)先判断出使△BOC的周长最小的点C的位置,再求解即可;
(3)分OA为对角线、为边这两种情况进行讨论计算即可得出答案.
(1)如图所示,过点B作BD⊥x轴于点D,
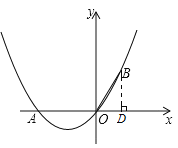
∵点A的坐标为(-2,0),OB=OA,
∴OB=OA=2,
∵∠AOB=120°,
∴∠BOD=60°,
在Rt△OBD中,∠ODB=90°,
∴∠OBD=30°,
∴OD=1,DB=![]() ,
,
∴点B的坐标是(1, ![]() ),
),
设所求抛物线的解析式为y=ax2+bx+c,
由已知可得:
 ,
,
解得: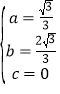
∴所求抛物线解析式为![]() ;
;
(2)存在.
如图所示,
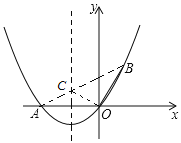
∵△BOC的周长=OB+BC+CO,
又∵OB=2,
∴要使△BOC的周长最小,必须BC+CO最小,
∵点O和点A关于对称轴对称,
∴连接AB与对称轴的交点即为点C,
由对称可知,OC=OA,
此时△BOC的周长=OB+BC+CO=OB+BC+AC;
点C为直线AB与抛物线对称轴的交点,
设直线AB的解析式为y=kx+b,
将点A(2,0),B(1,![]() )分别代入,得:
)分别代入,得:
![]() ,
,
解得: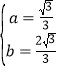 ,
,
∴直线AB的解析式为y=![]() x+
x+![]() ,
,
当x=1时span>,y=![]() ,
,
∴所求点C的坐标为(1,![]() );
);
(3)如图所示,
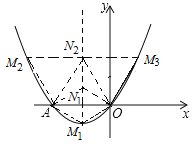
①当以OA为对角线时,
∵OA与MN互相垂直且平分,
∴点M1(1,![]() ),
),
②当以OA为边时,
∵OA=MN且OA∥MN,
即MN=2,MN∥x轴,
设N(1,t),
则M(3,t)或(1,t)
将M点坐标代入![]() ,
,
解得,t=![]() ,
,
∴M2(3,![]() ),M3 (1,
),M3 (1,![]() )
)
综上:点M的坐标为:(-1,-![]() ),或(-3,
),或(-3,![]() )或(1,
)或(1,![]() ).
).


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
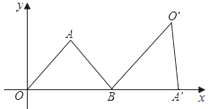
【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
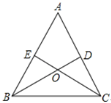
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
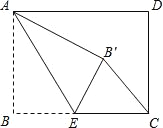
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如果两个角的差的绝对值等90°,就可以称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1﹣∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角),如图,OC⊥AB于点O,OE⊥OD,图中所有互为垂角的角有( )
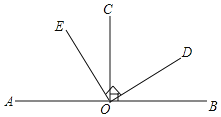
A.2对B.3对C.4对D.6对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若从 -3,-1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组![]() 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线![]() 上的概率是_________.
上的概率是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行,本届论坛期间,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区. 已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com