练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】我们定义：如果两个角的差的绝对值等90°，就可以称这两个角互为垂角，例如：∠1＝120°，∠2＝30°，|∠1﹣∠2|＝90°，则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角)，如图，OC⊥AB于点O，OE⊥OD，图中所有互为垂角的角有( )

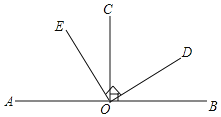
    A.2对B.3对C.4对D.6对

    【答案】C

    【解析】

    根据互为垂角的定义即可求解，以及OC⊥AB于点O，OE⊥OD，即可找到图中互为垂角的角.

    解：∵OC⊥AB，OE⊥OD，

    |∠EOB-∠DOB|=90°，|∠EOB-∠EOC|=90°，|∠AOD-∠COD|=90°，

    |∠AOD-∠AOE|=90°；

    所以互为垂角的角有4对：∠EOB与∠DOB，∠EOB与∠EOC，∠AOD与∠COD，∠AOD与∠AOE；

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

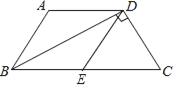
    【题目】已知：如图，四边形ABCD中，AD∥BC，对角线BD平分∠ABC，且BD⊥DC，E为BC中点，AB＝DE．

    （1）求证：四边形ABED是菱形；

    （2）若∠C＝60°，CD＝4，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若有理数a，b满足条件：（m是整数），则称有理数a，b为一对“共享数”，其中整数m是a，b的“共享因子”．

    （1）下列两对数中：①3和5，②6和8，是一对“共享数”的是　 　；（填序号）

    （2）若7和x是一对“共享数”，且“共享因子”为2，求x的值；

    （3）探究：当有理数a，b满足什么条件时，a，b是一对“共享数”．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，的两边分别平行．

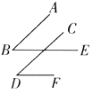
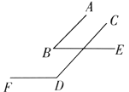
    ① ②

    （1）在图①中，与的数量关系是什么？为什么？

    （2）在图②中，与的数量关系是什么？为什么？

    （3）由（1）（2）可得结论：________；

    （4）应用：若两个角的两边两两互相平行,其中一个角比另一个角的2倍少,求这两个角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD的面积为10cm2，它的两条对角线交于点O1，以AB、AO1为两邻边作平行四边形ABC1O1，平行四边形ABC1O1的对角线交于点O2，同样以AB、AO2为两邻边作平行四边形ABC2O2，…，依此类推，则平行四边形ABCnOn的面积为( )

    A. cm2B. cm2C. cm2D. cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

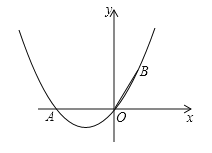
    【题目】如图，在直角坐标系中，点A的坐标为（-2，0），OB=OA，且∠AOB=120°．

    （1）求经过A、O、B三点的抛物线的解析式；

    （2）在（1）中抛物线的对称轴上是否存在点C，使△OBC的周长最小？若存在，求出点C的坐标；若不存在，请说明理由；

    （3）若点M为抛物线上一点，点N为对称轴上一点，是否存在点M、N使得A、O、M、N构成的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）

    甲

    乙

    进价（元/件）

    22

    30

    售价（元/件）

    29

    40

    （1）该超市购进甲、乙两种商品各多少件？

    （2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

    （3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙商品是按原价打几折销售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点；直线与轴交于点，与直线交于点，且点的纵坐标为4.

    （1）不等式的解集是 ；

    （2）求直线的解析式及的面积；

    （3）点在坐标平面内，若以、、、为顶点的四边形是平行四边形，求符合条件的所有点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①,已知线段AB=12 cm,点C为AB上的一个动点,点D,E分别是AC和BC的中点.

    (1)若点C恰好是AB中点,则DE=_____cm.

    (2)若AC=4 cm,求DE的长；

    (3)试利用“字母代替数”的方法，说明不论AC取何值(不超过12 cm)，DE的长不变；

    (4)知识迁移：如图②,已知∠AOB=120°,过角的内部任一点C画射线OC，若OD，OE分别平分∠AOC和∠BOC，试说明∠DOE=60°与射线OC的位置无关.

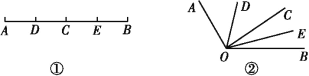
    查看答案和解析>>

    同步练习册答案