
【题目】如图,在![]() 中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②
中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
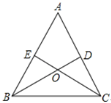
(1)上述三个条件中,由哪两个条件可以判定![]() 是等腰三角形?(用序号写出所有成立的情形)
是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,说明你的理由.
【答案】(1)①②或①③;(2)见解析.
【解析】
(1)由①②;①③.两个条件可以判定△ABC是等腰三角形,
(2)先求出∠ABC=∠ACB,即可证明△ABC是等腰三角形.
解:(1)①②;①③.
(2)选①③证明如下,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
又∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
选①②证明如下,
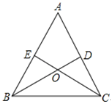
在△EBO与△DCO中,
∵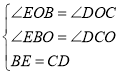 ,
,
∴△EBO≌△DCO(AAS),
∴OB=OC,
∴∠OBC=∠OCB,
∵∠EBO=∠DCO,
又∵∠ABC=∠EBO+∠OBC,∠ACB=∠DCO+∠OCB,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动,他从A处出发去看望B、C、D处的其他甲虫,规定:向上向右走均为正,向下向左走均为负,如果从A到B记为A→B{1,4},从B到A记为:B→A{﹣1,﹣4},其中第一个数表示左右方向,第二个数表示上下方向.
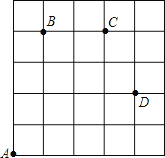
(1)图中A→C{ , },C→B{ , }.
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(3)若图中另有两个格点M、N,且M→A{2﹣a,b﹣3},M→N{3﹣a,b﹣2},则N→A应记为什么?直接写出你的答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知射线OA,OB,OC,OD,∠AOD=∠BOC=α.
①若α=38°,∠COD=30°,求∠BOD、∠AOC的度数;
②若∠COD=25°,请找出图中与∠BOD相等的角,并通过计算说明理由;
(2)如图2,∠MPN是钝角,请利用三角尺画特殊角的功能,在图2中画一个与∠MPN相等的角.(标出图中特殊角的度数,并写出与∠MPN相等的角)
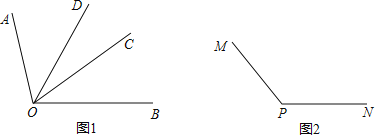
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若有理数a,b满足条件:![]() (m是整数),则称有理数a,b为一对“共享数”,其中整数m是a,b的“共享因子”.
(m是整数),则称有理数a,b为一对“共享数”,其中整数m是a,b的“共享因子”.
(1)下列两对数中:①3和5,②6和8,是一对“共享数”的是 ;(填序号)
(2)若7和x是一对“共享数”,且“共享因子”为2,求x的值;
(3)探究:当有理数a,b满足什么条件时,a,b是一对“共享数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.
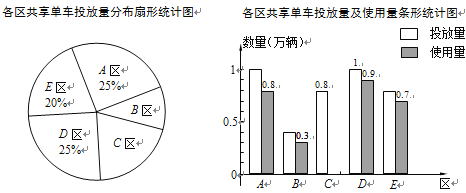
(1)该公司在全市一共投放了 万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为 °;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 的两边分别平行.
的两边分别平行.
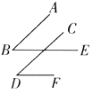
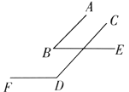
① ②
(1)在图①中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(2)在图②中,![]() 与
与![]() 的数量关系是什么?为什么?
的数量关系是什么?为什么?
(3)由(1)(2)可得结论:________;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少![]() ,求这两个角的度数.
,求这两个角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A的坐标为(-2,0),OB=OA,且∠AOB=120°.
(1)求经过A、O、B三点的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使△OBC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)若点M为抛物线上一点,点N为对称轴上一点,是否存在点M、N使得A、O、M、N构成的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
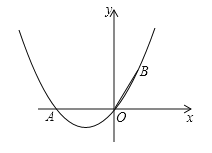
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中网格上按要求画出图形,并回答问题:
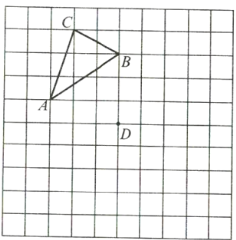
(1)如果将三角形![]() 平移,使得点
平移,使得点![]() 平移到图中点
平移到图中点![]() 位置,点
位置,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,请画出三角形
,请画出三角形![]() ;
;
(2)画出三角形![]() 关于点
关于点![]() 成中心对称的三角形
成中心对称的三角形![]() .
.
(3)三角形![]() 与三角形
与三角形![]() ______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点
______(填“是”或“否”)关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com