【题目】如图1，在菱形ABCD中，AC=2，BD=2，AC，BD相交于点O．
（1）求边AB的长；
（2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别与边BC，CD相交于点E，F，连接EF与AC相交于点G．
①判断△AEF是哪一种特殊三角形，并说明理由；
②旋转过程中，当点E为边BC的四等分点时（BE＞CE），求CG的长．

参考答案：

【答案】（1）2 （2）①等边三角形 ②

【解析】试题分析：（1）∵四边形ABCD是菱形，

∴△AOB为直角三角形，且OA=AC=1，OB=BD=．

在Rt△AOB中，由勾股定理得：

AB===2．

（2）①△AEF是等边三角形．理由如下：

∵由（1）知，菱形边长为2，AC=2，

∴△ABC与△ACD均为等边三角形，

∴∠BAC=∠BAE+∠CAE=60°，又∠EAF=∠CAF+∠CAE=60°，

∴∠BAE=∠CAF．

在△ABE与△ACF中，

∵，

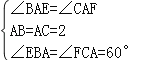∴△ABE≌△ACF（ASA），

∴AE=AF，

∴△AEF是等腰三角形，

又∵∠EAF=60°，

∴△AEF是等边三角形．

②BC=2，E为四等分点，且BE＞CE，

∴CE=，BE=．

由①知△ABE≌△ACF，

∴CF=BE=．

∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°（三角形内角和定理），

∠AEG=∠FCG=60°（等边三角形内角），

∠EGA=∠CGF（对顶角）

∴∠EAC=∠GFC．

在△CAE与△CFG中，

∵，

∴△CAE∽△CFG（AA），

∴，即，

解得：CG=．

关闭