【题目】甲乙两人同时登西山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图像如图所示，根据图像所提供的信息解答下列问题：
（1）甲登山的速度是每分钟米，乙在A地提速时距地面的高度b为米．
（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度y（米）与登山时间x（分）之间的函数关系式．
（3）登山多长时间时，乙追上了甲此时乙距A地的高度为多少米？

参考答案：

【答案】
（1）10；30
（2）解：由图知：x= +2=11，

∵C（0，100），D（20，300）

∴线段CD的解析式：y甲=10x+100（0≤x≤20）；

∵A（2，30），B（11，300），

∴折线OAB的解析式为：y乙=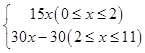


（3）解：由 ，

解得 ，

∴登山6.5分钟时乙追上甲．

此时乙距A地高度为165﹣30=135（米）


【解析】解：（1）甲的速度为：（300﹣100）÷20=10米/分， 根据图中信息知道乙一分的时间，走了15米，
那么2分时，将走30米；（1）甲的速度=（300﹣100）÷20=10，根据图像知道一分的时间，走了15米，然后即可求出A地提速时距地面的高度；（2）乙提速后，乙的速度是甲登山速度的3倍，所以乙的速度是30米/分．那么求出点B的坐标，加上点A的坐标代入一次函数解析式即可求出乙的函数解析式，把C、D坐标代入一次函数解析式可求出甲的函数解析式；（3）乙追上了甲即此时的y的值相等，然后求出时间在计算距A地的高度．

关闭