
分析 根据题意将原式变形得出关于p,q的方程组,进而得出答案.
解答 解:∵(2,3)⊕(p,q)=(4,32),
∴(2p-3q,2q+3p)=(4,32),
∴$\left\{\begin{array}{l}{2q-3p=4}\\{2q+3p=32}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{q=9}\\{p=\frac{14}{3}}\end{array}\right.$,
故p=$\frac{14}{3}$,q=9.
故答案为:9,$\frac{14}{3}$.
点评 此题主要考查了实数运算,正确将原式变形得出p,q的方程组是解题关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:选择题
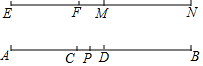 如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )
如图,已知线段EF=3,线段MN=4,线段AB=11,用圆规在线段AB上截取AC=EF,BD=MN,P是线段CD的中点,则AP的长度为( )| A. | 4 | B. | 5 | C. | 5.5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com