
【题目】设x是实数,现在我们用{x}表示不小于x的最小整数,如{3.2}=4,{﹣2.6}=﹣2,{4}=4,{﹣5}=5.在此规定下任一实数都能写出如下形式:x={x}﹣b,其中0≤b<1.
(1)直接写出{x}与x,x+1的大小关系是 (由小到大);
(2)根据(1)中的关系式解决下列问题:
①求满足{3x+11}=6的x的取值范围;
②解方程:{3.5x+2}=2x﹣![]() .
.
【答案】(1)x≤{x}<x+1,(2)①﹣2<x≤﹣![]() ,②x=﹣
,②x=﹣![]() ,
,
【解析】
(1)x={x}﹣b,其中0≤b<1,b={x}﹣x,即0≤{x}﹣x<1,即可判断三者的大小关系,
(2)根据(1)中的关系得到关于x的一元一次不等式组,解之即可,
②根据(1)中的关系得到关于x的一元一次不等式组,且2x﹣![]() 为整数,即可求解.
为整数,即可求解.
(1)∵x={x}﹣b,其中0≤b<1,
∴b={x}﹣x,
即0≤{x}﹣x<1,
∴x≤{x}<x+1,
故答案为:x≤{x}<x+1,
(2)①∵{3x+11}=6,
∴3x+11≤6<(3x+11)+1,
解得:﹣2<x≤﹣![]() ,
,
即满足{3x+11}=6的x的取值范围为:﹣2<x≤﹣![]() ,
,
②∵{3.5x+2}=2x﹣![]() ,
,
∴3.5x+2≤2x﹣![]() <(3.5x+2)+1,且2x﹣
<(3.5x+2)+1,且2x﹣![]() 为整数,
为整数,
解不等式组得:﹣![]() <x≤﹣
<x≤﹣![]() ,
,
∴﹣![]() <2x﹣
<2x﹣![]() ≤﹣3
≤﹣3![]() ,整数2x﹣
,整数2x﹣![]() 为﹣4,
为﹣4,
解得:x=﹣![]() ,
,
即原方程的解为:x=﹣![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中不一定成立的是( )

A. S△BEC=2S△CEF B. EF=CF
C. ∠DCF=![]() ∠BCD D. ∠DFE=3∠AEF
∠BCD D. ∠DFE=3∠AEF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(﹣1,t),B(3,t),与y轴交于点C(0,﹣1).一次函数y=x+n的图象经过抛物线的顶点D.
(1)求抛物线的表达式;
(2)求一次函数y=x+n的表达式;
(3)将直线l:y=mx+n绕其与y轴的交点E旋转,使当﹣1≤x≤1时,直线l总位于抛物线的下方,请结合函数图象,求m的取值范围.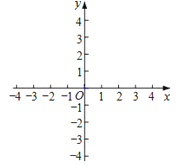
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为100° 的菱形,剪口与折痕所成的角的度数应为( )
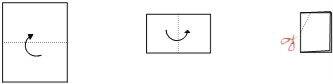
A. 25°或50° B. 20°或50° C. 40°或50° D. 40°或80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF ;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b是多项式2m2n-m3n2-m-2的次数,c是单项式-2xy2的系数,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P,Q同时从A,B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图放置 其中∠ACB=∠DEC=90,∠A=45,∠D=30,斜边 AB=4,CD=5,把三角板DCE绕点C顺时针旋转15得到三角形D1CE (如图二),此时AB与CD1交于点O,则线段AD1的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机从箱子里取出1个球,则取出黄球的概率是多少?
(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com