
【题目】已知a是最大的负整数,b是多项式2m2n-m3n2-m-2的次数,c是单项式-2xy2的系数,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P,Q同时从A,B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由)
【答案】(1)a=-1,b=5,c=-2(2)运动4秒后,点Q可以追上点P(3)存在点M, M对应的数是2或-2![]()
【解析】
(1)观察题目,理解多项式和单项式的相关概念,解题的关键是画出数轴,正确在数轴上找到所对应的点;注意最大的负整数是-1,单项式的系数是单项式中的数字因数,多项式的次数是多项式中最高次项的次数;
(2)根据数轴上两点间的距离的求法进行求解即可;
(3)数轴上两点间的距离公式:两点所对应的数的差的绝对值,据此进行求解即可
(1)![]() ,如图
,如图
![]()
(2)因为动点P,Q同时从A,B出发沿数轴负方向运动,点P的速度是每秒![]() 个单位长度,点Q的速度是每秒2个单位长度,又因为
个单位长度,点Q的速度是每秒2个单位长度,又因为![]() ,两点速度差为:
,两点速度差为:![]() ,所以
,所以![]() ,运动4秒后,点Q可以追上点P
,运动4秒后,点Q可以追上点P
(3)存在点M,使P到A,B,C的距离和等于10,当M在AB之间,则M对应的数是2;当M在C点左侧,则M对应的数是![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,第2017次移动到点A2017时,A2017在数轴上对应的实数是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程4(2﹣x)+x=ax的解为正整数,且关于x的不等式组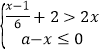 有解,则满足条件的所有整数a的值之和是( )
有解,则满足条件的所有整数a的值之和是( )
A. 4 B. 0 C. ﹣1 D. ﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x是实数,现在我们用{x}表示不小于x的最小整数,如{3.2}=4,{﹣2.6}=﹣2,{4}=4,{﹣5}=5.在此规定下任一实数都能写出如下形式:x={x}﹣b,其中0≤b<1.
(1)直接写出{x}与x,x+1的大小关系是 (由小到大);
(2)根据(1)中的关系式解决下列问题:
①求满足{3x+11}=6的x的取值范围;
②解方程:{3.5x+2}=2x﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a、b,定义一种运算“![]() ”为:ab=a2 +ab-2,有下列命题:
”为:ab=a2 +ab-2,有下列命题:
①1![]() 3=2;
3=2;
②方程x![]() 1=0的根为:x1 =-2,x2 =1;
1=0的根为:x1 =-2,x2 =1;
③不等式组 ![]() 的解集为:-1<x<4;
的解集为:-1<x<4;
④点(![]() ,
,![]() )在函数y=x
)在函数y=x![]() (-1)的图象上.
(-1)的图象上.
其中正确的是( )
A. ①②③④ B. ①③ C. ①②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;
(2)若AB=12,AD=8,CD=15,求DB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
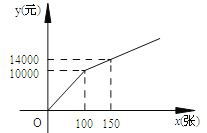
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=﹣![]() x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
x+m与y轴交于点A(0,6),直线l2:y=kx+1分别与x轴交于点B(﹣2,0),与y轴交于点C,两条直线交点记为D.
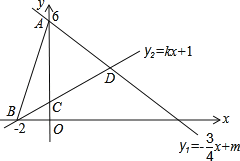
(1)m= ,k= ;
(2)求两直线交点D的坐标;
(3)根据图象直接写出y1<y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
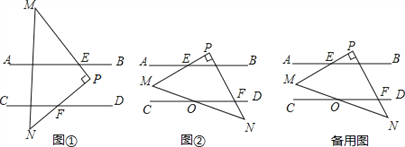
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com