
 ;⑤DG:GB=1:2
;⑤DG:GB=1:2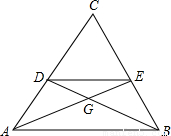
 AB,DE∥AB,进而可得①②的正误;再根据相似三角形的面积之比等于对应边之比的平方可判断出③的正误;再根据梯形的中位线定理可计算出④的正误,然后再证明△DEG∽△BAG,再根据相似三角形的性质可判断出⑤.
AB,DE∥AB,进而可得①②的正误;再根据相似三角形的面积之比等于对应边之比的平方可判断出③的正误;再根据梯形的中位线定理可计算出④的正误,然后再证明△DEG∽△BAG,再根据相似三角形的性质可判断出⑤. AB,DE∥AB,
AB,DE∥AB,
 =
= ,
, =
= ,
, (AB+DE)=
(AB+DE)= ,
, =
= =
= ,
,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
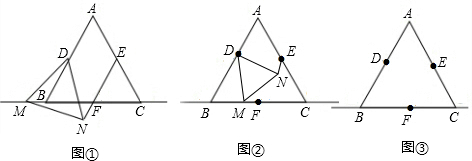
 23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.
23、如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点.查看答案和解析>>
科目:初中数学 来源: 题型:
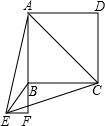 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.
如图,已知等边三角形△AEC,以AC为对角线做正方形ABCD(点B在△AEC内,点D在△AEC外).连接EB,过E作EF⊥AB,交AB的延长线为F.请猜测直线BE和直线AC的位置关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动| 10 |
| 3 |
| 10 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com