
 如图,AD是△ABC的边BC上的高,有以下四个条件:①∠BAD=∠ACD;②∠BAD=∠CAD;③AB=AC;④BD=CD.添加以上四个条件中的某一个就能推出△ABC是等腰三角形的是②③④(把所有正确答案的序号都填写在横线上)
如图,AD是△ABC的边BC上的高,有以下四个条件:①∠BAD=∠ACD;②∠BAD=∠CAD;③AB=AC;④BD=CD.添加以上四个条件中的某一个就能推出△ABC是等腰三角形的是②③④(把所有正确答案的序号都填写在横线上) 科目:初中数学 来源: 题型:选择题
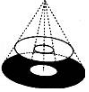 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)元 | B. | (3a+2b)元 | C. | 5(a+b)元 | D. | (2a+3b)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,点C在边AD上,连接BD.
如图,在Rt△ABC和Rt△ADE中,AB=AD,AC=AE,∠ACB=∠AED=90°,点C在边AD上,连接BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com