
ЁОЬтФПЁП(1)ШчЭМ(1),вбжЊЃКдкЁїABCжа,ЁЯBAC=90Ёу,AB=AC,жБЯпmОЙ§ЕуA,BDЁЭжБЯпm,CEЁЭжБЯпm,ДЙзуЗжБ№ЮЊЕуD,жЄУї:ЁїABDЁеЁїACEЃЌDE=BD+CEЃЛ
(2)ШчЭМ(2),НЋ(1)жаЕФЬѕМўИФЮЊЃКдкЁїABCжаЃЌAB=ACЃЌD, A, EШ§ЕуЖМдкжБЯпmЩЯЃЌВЂЧвгаЁЯBDA=ЁЯAEC=ЁЯBAC=aЃЌЦфжаaЮЊШЮвтШёНЧЛђЖлНЧЃЌЧыЮЪНсТлDE=BD+CEЪЧЗёГЩСЂ?ШчГЩСЂЃЌЧыФуИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩ.
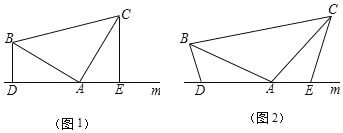
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)ГЩСЂЃЌРэгЩМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнBDЁЭжБЯпmЃЌCEЁЭжБЯпmЕУЁЯBDA=ЁЯCEA=90ЁуЃЌЖјЁЯBAC=90ЁуЃЌИљОнЕШНЧЕФгрНЧЯрЕШЕУЁЯCAE=ЁЯABDЃЌШЛКѓИљОнЁАAASЁБПЩХаЖЯЁїADBЁеЁїCEAЃЌ
дђAE=BDЃЌAD=CEЃЌгкЪЧDE=AE+AD=BD+CEЃЛ
ЃЈ2ЃЉРћгУЁЯBDA=ЁЯBAC=ІСЃЌдђЁЯDBA+ЁЯBAD=ЁЯBAD+ЁЯCAE=180Ёу-ІСЃЌЕУГіЁЯCAE=ЁЯABDЃЌНјЖјЕУГіЁїADBЁеЁїCEAМДПЩЕУГіД№АИЃЎ
(1)ЁпBDЁЭжБЯпmЃЌCEЁЭжБЯпmЃЌ
ЁрЁЯBDA=ЁЯCEA=90ЁуЃЌ
ЁпЁЯBAC=90Ёу
ЁрЁЯBAD+ЁЯCAE=90ЁуЃЌ
ЁпЁЯBAD+ЁЯABD=90ЁуЃЌ
ЁрЁЯCAE=ЁЯABDЃЌ
ЁпдкЁїADBКЭЁїCEAжа
ЁрЁїADBЁеЁїCEA(AAS)ЃЌ
ЁрAE=BDЃЌAD=CEЃЌ
ЁрDE=AE+AD=BD+CEЃЛ
(2)ЁпЁЯBDA=ЁЯBAC=ІСЃЌ
ЁрЁЯDBA+ЁЯBAD=ЁЯBAD+ЁЯCAE=180ЁуІСЃЌ
ЁрЁЯCAE=ЁЯABDЃЌ
ЁпдкЁїADBКЭЁїCEAжа
 ЃЌ
ЃЌ
ЁрЁїADBЁеЁїCEA(AAS)ЃЌ
ЁрAE=BDЃЌAD=CEЃЌ
ЁрDE=AE+AD=BD+CE.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌЫФБпаЮABCDжаЃЌAB=3cmЃЌAD=4cmЃЌBC=13cmЃЌCD=12cmЃЌЧвЁЯA=90ЁуЃЌЧѓЫФБпаЮABCDЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
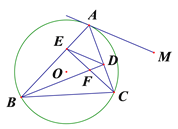
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЌCEЁЭABгкЕуEЃЌBDЁЭACгкЕуDЃЌBDЁЂCEЯрНЛгкЕуFЃЌСЌНсEDЃЎ
(1)ШєЁЯABC=45Ёу,жЄУїAE=EFЃЛ
(2)ЧѓжЄЃКЁїAEDЁзЁїACBЃЛ
(3)Й§ЕуAЕФжБЯпAMЁЮEDЃЌ AMЪЧЁбOЕФЧаЯпТ№ЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№БэЪОаЁУїВНаагыаЁИеЦяГЕдкЭЌвЛТЗЩЯааЪЛЕФТЗГЬSгыЪБМфtЕФЙиЯЕЃЎ
ЗжБ№БэЪОаЁУїВНаагыаЁИеЦяГЕдкЭЌвЛТЗЩЯааЪЛЕФТЗГЬSгыЪБМфtЕФЙиЯЕЃЎ
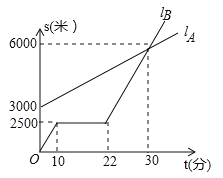
ЃЈ1ЃЉаЁИеГіЗЂЪБгыаЁУїЯрОр________УзЃЎзпСЫвЛЖЮТЗКѓЃЌздааГЕЗЂЩњЙЪеЯНјаааоРэЃЌЫљгУЕФЪБМфЪЧ________ЗжжгЃЎ
ЃЈ2ЃЉЧѓГіаЁУїаазпЕФТЗГЬSгыЪБМфtЕФКЏЪ§ЙиЯЕЪНЃЎЃЈаДГіМЦЫуЙ§ГЬЃЉ
ЃЈ3ЃЉЧыЭЈЙ§МЦЫуЫЕУїЃКШєаЁИеЕФздааГЕВЛЗЂЩњЙЪеЯЃЌБЃГжГіЗЂЪБЕФЫйЖШЧАНјЃЌКЮЪБгыаЁУїЯргіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЃЈ5mn2Љ4m2nЃЉЃЈЉ2mnЃЉ
ЃЈ2ЃЉЃЈx+7ЃЉЃЈxЉ6ЃЉЉЃЈxЉ2ЃЉЃЈx+1ЃЉ
ЃЈ3ЃЉ (Ѓ![]() )2 016ЁС161 008ЃЛ
)2 016ЁС161 008ЃЛ
ЁОД№АИЁПЃЈ1ЃЉЉ10m2n3+8m3n2ЃЛЃЈ2ЃЉ2xЉ40ЃЛ(3)1ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉдЪНРћгУЕЅЯюЪНГЫвдЖрЯюЪНЗЈдђМЦЫуМДПЩЕУЕННсЙћЃЛ
ЃЈ2ЃЉдЪНСНЯюРћгУЖрЯюЪНГЫвдЖрЯюЪНЗЈдђМЦЫуЃЌШЅРЈКХКЯВЂМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉЯШИљОнУнЕФГЫЗНЕФФцдЫЫуЃЌАб(Ѓ![]() )2 016ЛЏЮЊ(
)2 016ЛЏЮЊ(![]() )1008ЃЌдйИљОнЛ§ЕФГЫЗНЕФФцдЫЫуМЦЫуМДПЩ.
)1008ЃЌдйИљОнЛ§ЕФГЫЗНЕФФцдЫЫуМЦЫуМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉдЪН=ЃЈ5mn2ЃЉЃЈЉ2mnЃЉ+ЃЈЉ4m2nЃЉЃЈЉ2mnЃЉ=Љ10m2n3+8m3n2ЃЛ
ЃЈ2ЃЉдЪН=x2Љ6x+7xЉ42Љx2Љx+2x+2=2xЉ40ЃЎ
ЃЈ3ЃЉдЪН=(![]() )1008ЁС161 008=(
)1008ЁС161 008=(![]() ЁС16)1 008=1.
ЁС16)1 008=1.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
19
ЁОЬтФПЁПШчЭМЃЌЗНИёЭМжаУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЌЕуAЁЂBЁЂCЖМЪЧИёЕуЃЎ
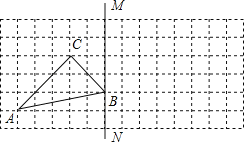
ЃЈ1ЃЉЛГіЁїABCЙигкжБЯпBMЖдГЦЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉаДГіAA1ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌAB=4ЃЌAD=3ЃЌелЕўжНЦЌЪЙDAгыЖдНЧЯпDBжиКЯЃЌЕуAТфдкЕуAЁфДІЃЌелКлЮЊDEЃЌдђAЁфEЕФГЄЪЧЃЈЁЁЁЁЃЉ
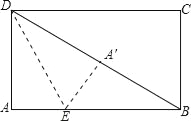
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЫМПМЃК
Ъ§бЇПЮЩЯРЯЪІГіСЫвЛЕРЗжЪНЛЏМђЧѓжЕЬтФПЃЎ
ЬтФПЃК ![]() ЁТ(xЃЋ1)ЁЄ
ЁТ(xЃЋ1)ЁЄ![]() Ѓ
Ѓ![]() ЃЌЦфжаxЃНЃ
ЃЌЦфжаxЃНЃ![]() .
.
ЁАЧкЗмЁБаЁзщЕФбюУїЭЌбЇеЙЪОСЫЫћЕФНтЗЈЃК
НтЃКдЪНЃН![]() Ѓ
Ѓ![]() .........................................................................ЕквЛВН
.........................................................................ЕквЛВН
ЃН![]() Ѓ
Ѓ ..........................................................................ЕкЖўВН
..........................................................................ЕкЖўВН
ЃН![]() ...........................................................................................ЕкШ§ВН
...........................................................................................ЕкШ§ВН
ЃН![]() ..................................................................................................ЕкЫФВН
..................................................................................................ЕкЫФВН
ЕБxЃНЃ![]() ЪБЃЌдЪНЃН
ЪБЃЌдЪНЃН .................................................................ЕкЮхВН
.................................................................ЕкЮхВН
ЧыФуШЯецдФЖСЩЯЪіНтЬтЙ§ГЬЃЌВЂЛиД№ЮЪЬтЃК
ФуШЯЮЊИУЭЌбЇЕФНтЗЈе§ШЗТ№ЃПШчгаДэЮѓЃЌЧыжИГіДэЮѓдкЕкМИВНЃЌВЂаДГіЭъећЁЂе§ШЗЕФНтД№Й§ГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЫвПЭТжЭЌЪБРыПЊИлПкЃЌКНааЕФЫйЖШЖМЪЧ40m/minЃЌМзПЭТжгУ15minЕНДяЕуAЃЌввПЭТжгУ20minЕНДяЕуBЃЌШєAЃЌBСНЕуЕФжБЯпОрРыЮЊ1000mЃЌМзПЭТжбизХББЦЋЖЋ30ЁуЕФЗНЯђКНааЃЌдђввПЭТжЕФКНааЗНЯђПЩФмЪЧЃЈЁЁЁЁЃЉ
A. ББЦЋЮї30Ёу B. ФЯЦЋЮї30Ёу C. ФЯЦЋЖЋ60Ёу D. ФЯЦЋЮї60Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ3ЃЉЁЂЃЈЉ4ЃЌ1ЃЉЁЂЃЈЉ2ЃЌ1ЃЉЃЌНЋЁїABCбивЛШЗЖЈЗНЯђЦНвЦЕУЕНЁїA1B1C1ЃЌЕуBЕФЖдгІЕуB1ЕФзјБъЪЧЃЈ1ЃЌ2ЃЉЃЌдђЕуA1ЃЌC1ЕФзјБъЗжБ№ЪЧ ЃЈЁЁЁЁЃЉ
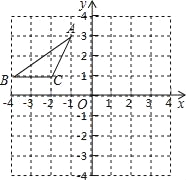
A. A1ЃЈ4ЃЌ4ЃЉЃЌC1ЃЈ3ЃЌ2ЃЉ B. A1ЃЈ3ЃЌ3ЃЉЃЌC1ЃЈ2ЃЌ1ЃЉ C. A1ЃЈ4ЃЌ3ЃЉЃЌC1ЃЈ2ЃЌ3ЃЉ D. A1ЃЈ3ЃЌ4ЃЉЃЌC1ЃЈ2ЃЌ2ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com