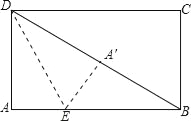
[题目]如图.在矩形纸片ABCD中.AB=4.AD=3.折叠纸片使DA与对角线DB重合.点A落在点A′处.折痕为DE.则A′E的长是( )A. 1 B. C. D. 2 题目和参考答案——青夏教育精英家教网—

【题目】如图，在矩形纸片ABCD中，AB=4，AD=3，折叠纸片使DA与对角线DB重合，点A落在点A′处，折痕为DE，则A′E的长是（　　）

A. 1 B. C. D. 2

【答案】C

【解析】分析：由在矩形纸片ABCD中，AB=4，AD=3，可求得BD的长，由折叠的性质，即可求得A′B的长，然后设A′E=x，由勾股定理即可得：x2+4=（4﹣x）2，解此方程即可求得答案．

详解：∵四边形ABCD是矩形，∴∠A=90°，∴BD==5，由折叠的性质，可得：A′D=AD=3，A′E=AE，∠DA′E=90°，∴A′B=BD﹣A′D=5﹣3=2，设A′E=x，则AE=x，BE=AB﹣AE=4﹣x．在Rt△A′BE中，A′E2+A′B2=BE2，∴x2+4=（4﹣x）2，解得：x=，∴A′E=．

故选C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，在四边形ABCD中，AB=AD. ∠B+∠ADC=180°，点E，F分别在四边形ABCD的边BC，CD上，∠EAF=∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系.

图1 图2 图3

(1)思路梳理

将△ABE绕点A逆时针旋转至△ADG，使AB与AD重合.由∠B+∠ADC=180°，得∠FDG=180°，即点F，D，G三点共线. 易证△AFG ，故EF，BE，DF之间的数量关系为；

(2)类比引申

如图2，在图1的条件下，若点E，F由原来的位置分别变到四边形ABCD的边CB，DC的延长线上，∠EAF=∠BAD，连接EF，试猜想EF，BE，DF之间的数量关系，并给出证明.

(3)联想拓展

如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在边BC上，且∠DAE=45°. 若BD=1，EC=2，则DE的长为 .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，∠MON＝90°，点A，B分别在射线OM、ON上．将射线OA绕点O沿顺时针方向以每秒9°的速度旋转，同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2)．设旋转时间为t(0≤t≤40，单位秒)．

(1)当t＝8时，∠AOB＝　 °；

(2)在旋转过程中，当∠AOB＝36°时，求t的值．

(3)在旋转过程中，当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时，请求出t的值．

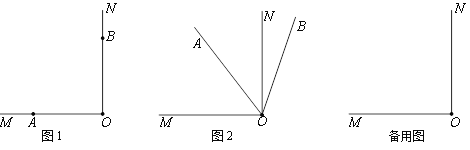
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知AB＝AC，PB＝PC，给出下面结论：①BP=CP，②EB＝EC，③AD⊥BC，④EA平分∠BEC，其中正确的结论有（　　）

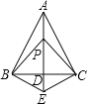
A.①②④B.①③④C.①②③D.①②③④

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】(1)如图(1),已知：在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE，DE=BD+CE；

(2)如图(2),将(1)中的条件改为：在△ABC中，AB=AC，D, A, E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=a，其中a为任意锐角或钝角，请问结论DE=BD+CE是否成立?如成立，请你给出证明；若不成立，请说明理由.

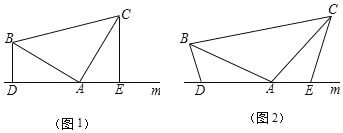
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）

A. ∠BCA=∠F； B. ∠B=∠E； C. BC∥EF ； D. ∠A=∠EDF

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．

(1)求证：△ABC是等腰三角形；

(2)判断点O是否在∠BAC的角平分线上，并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】永祚寺双塔，又名凌霄双塔，是山西省会太原现存古建筑中最高的建筑，位于太原市城区东南向山脚畔．数学活动小组的同学对其中一个塔进行了测量．测量方法如下：如图所示，间接测得该塔底部点B到地面上一点E的距离为48 m，塔的顶端为点A，且AB⊥CB，在点E处竖直放一根标杆，其顶端为D，在BE的延长线上找一点C，使C，D，A三点在同一直线上，测得CE＝2 m.

(1)方法1，已知标杆DE＝2.2 m，求该塔的高度；

(2)方法2，测量得∠ACB＝47.5°，已知tan47.5°≈1.09，求该塔的高度；

(3)假如该塔的高度在方法1和方法2测得的结果之间，你认为该塔的高度大约是多少米？