
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


【答案】(1)55m;(2)54.5m; (3)答案不唯一,如54.75 m或54.8 m
【解析】试题分析:(1)由题意,可得△ABC∽△DEC,根据相似三角形对应边的比等于相似比进行求解即可得;
(2)在Rt△ABC中,根据∠ACB的正切进行计算即可得;
(3)答案只要在上面两个小题的结果范围内即可.
试题解析:(1)由题意,可得△ABC∽△DEC,∴![]() ,
,
即![]() ,解得:AB=55,
,解得:AB=55,
答:该塔的高度为55m;
(2)在Rt△ABC中,tan∠ACB=![]() ,
,
∴AB=(48+2)×tan47.5°≈50×1.09=54.4(m),
答:该塔的高度为54.5m.
(3)答案不唯一,如54.75 m或54.8 m(数值在54.5~55之间均可).


科目:初中数学 来源: 题型:
【题目】几年前我国曾经流行有一种叫“二十四点”的数学趣味算题,方法是给出1~13之间的自然数,从中任取四个,将这四个数(四个数都只能用一次)进行“+”“-”“×”“÷”运算,可加括号使其结果等于24.
例如:对1,2,3,4可运算(1+2+3)×4=24,也可以写成4×(1+2+3)=24,但视作相同的方法.
现有郑、付两同学的手中分别握着四张扑克牌(见下图);若红桃、方块上的点数记为负数,黑桃、梅花上的点数记为正数.
请你对郑、付两同学的扑克牌的按要求进行记数,并按前面“二十四点”运算方式对郑、付两同学的记数分别进行列式计算,使其运算结果均为24.(分别尽可能提供多种算法)

依次记为:______ 、______ 、______ 、______

依次记为:______ 、______ 、______ 、______ .
(1)帮助郑同学列式计算:______
(2)帮助付同学列式计算:______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是( )
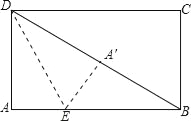
A. 1 B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线,

⑴写出所有∠EOC的补角 ;
⑵如果∠AOD=40°,求∠POF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学为了探索泥茶壶盛水喝起来凉的原因,对泥茶壶和塑料壶盛水散热情况进行对比实验.在同等情况下,把稍高于室温(25.5℃)的水放入凉壶中,每隔一小时同时测出凉壶水温,所得数据如下表:
刚倒入时 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
泥茶壶 | 34 | 27 | 25 | 23.5 | 23.0 | 22.5 | 22.5 | 22.5 |
塑料壶 | 34 | 30 | 27 | 26.0 | 25.5 | 22.5 | 22.5 | 22.5 |
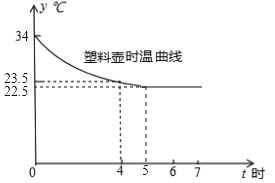
(1)塑料壶水温变化曲线如图,请在同一坐标系中,画出泥壶水温的变化曲线;
(2)比较泥壶和塑料壶水温变化情况的不同点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.

请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×![]() =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0).
(1)写出B点的坐标_____;
(2)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(3)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长春市市政工程中需要铺设一条长660米的管道,为了尽量减少施工对城市交通造成的影响,实际施工时,每天铺设管道的长度比原计划增加10%,结果提前6天完成,求实际每天铺设管道的长度与实际施工天数.某同学根据题意列出方程![]() ,则方程中未知数x所表示的量是( )
,则方程中未知数x所表示的量是( )
A. 原计划每天铺设管道的长度 B. 实际每天铺设管道的长度
C. 原计划施工的天数 D. 实际施工的天数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com