
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线,

⑴写出所有∠EOC的补角 ;
⑵如果∠AOD=40°,求∠POF的度数.
【答案】(1)∠EOD,∠AOF都是∠EOC的补角;(2)∠POD=70°.
【解析】
(1)首先根据垂直定义可得∠AOE=∠DOF=90°,然后再证明∠EOD=∠AOF,根据补角定义可得∠EOD,∠AOF都是∠EOC的补角;
(2)根据对顶角相等,可得∠BOC的度数,根据角平分线的定义,可得∠COP,根据余角的定义,可得答案.
(1)∵OE⊥AB,OF⊥CD,
∴∠AOE=∠DOF=90°,
∴∠EOA+∠AOD=∠DOF+∠AOD,
即:∠EOD=∠AOF,
∵∠EOC+∠EOD=180°,
∴∠AOF+∠EOC=180°,
∴∠EOD,∠AOF都是∠EOC的补角;
(2)由对顶角相等,得∠BOC=∠AOD=40°,
由OP是∠BOC的平分线,得∠COP=![]() ∠BOC=20°,
∠BOC=20°,
由余角的定义,得∠POD=∠COD-∠COP=90°-20°=70°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a、b满足![]() +|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
+|b-6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)a=______________,b=_____________,点B的坐标为_______________;
(2)当点P移动4秒时,请指出点P的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,PB=PC,给出下面结论:①BP=CP,②EB=EC,③AD⊥BC,④EA平分∠BEC,其中正确的结论有( )
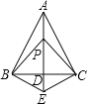
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 l 上有 A、B 两点,AB=12cm,点 O 是线段 AB 上的一点,OA=2OB.
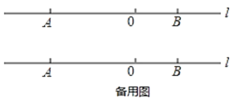
(1)OA=_______cm,OB=________cm;
(2)若点 C 是线段AB的中点,求线段 CO 的长;
(3)若动点 P、Q分别从 A、B同时出发,向右运动,点P的速度为2 厘米/秒,点Q的速度为1厘米/秒,设运动时间为x秒,当 x=_____秒时,PQ=4cm;
(4)有两条射线 OC、OD 均从射线 OA 同时绕点O顺时针方向旋转,OC旋转的速度为6度/秒,OD 旋转的速度为2度/秒.当OC与OD第一次重合时,OC、OD 同时停止旋转,设旋转时间为 t 秒,当t为何值时,射线OC⊥OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB∥CD,∠B=20°,∠D=110°.
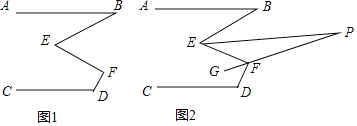
(1)若∠E=50°,请直接写出∠F的度数;
(2)探索∠E与∠F之间满足的数量关系,并说明理由;
(3)如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com