
【题目】抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0).
(1)写出B点的坐标_____;
(2)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(3)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
【答案】(3,0)
【解析】分析:(1)直接利用二次函数的对称性得出B点坐标即可;
(2)利用三角形面积求法结合抛物线上点的坐标性质得出答案;
(3)结合题意得出MD的函数关系式,进而得出答案.
详解:(1)∵抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0),
∴B点的坐标为:(3,0);
故答案为:(3,0);
(2)由抛物线y=ax2+bx+c的对称轴为直线x=1,A(﹣1,0),B(3,0),
则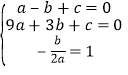 ,解得:
,解得: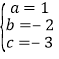 ,
,
故抛物线的表达式为y=x2﹣2x﹣3,
∴C(0,﹣3).
∴![]() .
.
∴S△POC=2S△BOC=9.
设点P的横坐标为xP,求得xP=±6.
代入抛物线的表达式,求得点P的坐标为(6,21),(﹣6,45).
(3)由点B(3,0),C(0,﹣3),得直线BC的表达式为y=x﹣3,

设点M(a,a﹣3),则点D(a,a2﹣2a﹣3).
∴MD=a﹣3﹣( a2﹣2a﹣3)
=﹣a2+3a
=![]() ,
,
∴当![]() 时,MD的最大值为
时,MD的最大值为![]() .
.


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,PB=PC,给出下面结论:①BP=CP,②EB=EC,③AD⊥BC,④EA平分∠BEC,其中正确的结论有( )
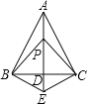
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永祚寺双塔,又名凌霄双塔,是山西省会太原现存古建筑中最高的建筑,位于太原市城区东南向山脚畔.数学活动小组的同学对其中一个塔进行了测量.测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为48 m,塔的顶端为点A,且AB⊥CB,在点E处竖直放一根标杆,其顶端为D,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得CE=2 m.
(1)方法1,已知标杆DE=2.2 m,求该塔的高度;
(2)方法2,测量得∠ACB=47.5°,已知tan47.5°≈1.09,求该塔的高度;
(3)假如该塔的高度在方法1和方法2测得的结果之间,你认为该塔的高度大约是多少米?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB∥CD,∠B=20°,∠D=110°.
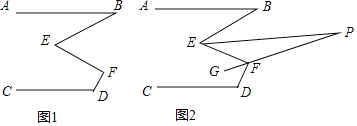
(1)若∠E=50°,请直接写出∠F的度数;
(2)探索∠E与∠F之间满足的数量关系,并说明理由;
(3)如图2,EP平分∠BEF,FG平分∠EFD,FG的反向延长线交EP于点P,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
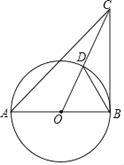
【题目】如图,在△ABC中,AB=BC,∠A=45°,以AB为直径的⊙O交CO于点D.
(1)求证:BC是⊙O的切线;
(2)连接BD,若BD=m,tan∠CBD=n,写出求直径AB的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)6a2-5a(a+2b-1)+a(-a+10b)+5,其中a=-1,b=2008;
(2)3xy2﹣[xy﹣2(2xy﹣![]() x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
x2y)+2xy2]+3x2y,其中x、y满足(x+2)2+|y﹣1|=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
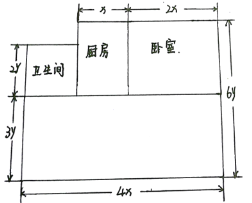
【题目】如图是一套房子的平面图,尺寸如图.
(1)这套房子的总面积是多少?(用含x、y的代数式表示)
(2)如果x=1.8米,y=1米,那么房子的面积是多少平方米?如果每平方米房价为5万元,那么房屋总价多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com