
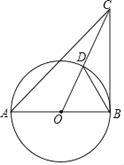
【题目】如图,在△ABC中,AB=BC,∠A=45°,以AB为直径的⊙O交CO于点D.
(1)求证:BC是⊙O的切线;
(2)连接BD,若BD=m,tan∠CBD=n,写出求直径AB的思路.
【答案】见解析
【解析】分析:(1)欲证明BC是⊙O的切线,只需推知∠ABC=90°即可;
(2)①连接AD,利用圆周角定理和等角的余角相等推知∠BAD=∠CBD;②通过解直角Rt△ABD可求AD=![]() ;③在Rt△ABD中,由勾股定理可求AB的长.
;③在Rt△ABD中,由勾股定理可求AB的长.
详解:(1)∵AB=BC,∠A=45°,
∴∠ACB=∠A=45°.
∴∠ABC=90°,
∴AB⊥BC,
∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)求解思路如下:
①连接AD,
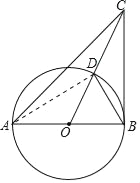
由AB为直径可知,∠ADB=90°,进而可知∠BAD=∠CBD;
②由BD=m,tan∠CBD=n,在Rt△ABD中,可求AD=![]() ;
;
③在Rt△ABD中,由勾股定理可求AB的长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 分别表示小明步行与小刚骑车在同一路上行驶的路程S与时间t的关系.
分别表示小明步行与小刚骑车在同一路上行驶的路程S与时间t的关系.
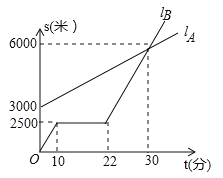
(1)小刚出发时与小明相距________米.走了一段路后,自行车发生故障进行修理,所用的时间是________分钟.
(2)求出小明行走的路程S与时间t的函数关系式.(写出计算过程)
(3)请通过计算说明:若小刚的自行车不发生故障,保持出发时的速度前进,何时与小明相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.

请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×![]() =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(﹣1,0).
(1)写出B点的坐标_____;
(2)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(3)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)、(﹣2,1),将△ABC沿一确定方向平移得到△A1B1C1,点B的对应点B1的坐标是(1,2),则点A1,C1的坐标分别是 ( )
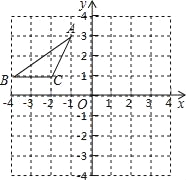
A. A1(4,4),C1(3,2) B. A1(3,3),C1(2,1) C. A1(4,3),C1(2,3) D. A1(3,4),C1(2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
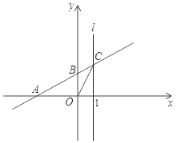
【题目】如图,已知点A(﹣3,0),点B(0,m),直线l:x=1.直线AB与直线l交于点C,连结OC.
(1)△OBC的面积与△OAC的面积比是否是定值?如果是,请求出面积比;如果不是,请说明理由.
(2)若m=2,点T在直线l上且TA=TB,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ADB=60°,∠CDB=50°.
(1)若AD∥BC,AB∥CD,求∠ABC的度数;
(2)若∠A=70°,请写出图中平行的线段,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com