
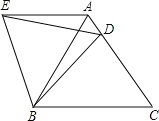
【题目】如图所示,在等边![]() 中,点D是边AC上一点,连接BD,将
中,点D是边AC上一点,连接BD,将![]() 绕着点B逆时针旋转
绕着点B逆时针旋转![]() ,得到
,得到![]() ,连接ED,则下列结论中:①
,连接ED,则下列结论中:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() ,其中正确结论的序号是
,其中正确结论的序号是![]()
![]()
A. ①② B. ①③ C. ②③ D. ①②④
【答案】D
【解析】
由题意可得∠EAB=∠ACB=∠ABC=60°,BD=BE,∠DBE=60°,可判断①②,根据三角形的外角等于不相邻的两个内角和可判断③④.
∵△ABC是等边三角形,∴AB=BC,∠BAC=∠ABC=∠ACB=60°,∠AEB=∠BDC.
∵将△BCD绕着点B逆时针旋转60°,得到△BAE,∴BE=BD,∠DBE=60°,∠EAB=∠ACB=60°,∴∠EAB=∠ABC=60°,△BED是等边三角形,∴AE∥BC.
∵△BED是等边三角形,∴∠DEB=60°,故①②正确;
∵∠AED+∠ADE+∠EAD=180°,∴∠AED+∠ADE=180°-120°=60°,∴∠ADE<60°.
∵∠BDC=∠BAC+∠ABD>60°,∴∠BDC≠∠ADE,故③错误;
∵∠AEB=∠BDC,∠AEB=∠AED+∠BED,∠BDC=∠BAC+∠ABD,∴∠AED=∠ABD,故④正确.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题,已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),
则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得n=-7,m=-21,
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
已知二次三项式3x2+5x-m有一个因式是(3x-1),求另一个因式以及m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
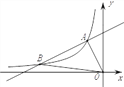
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
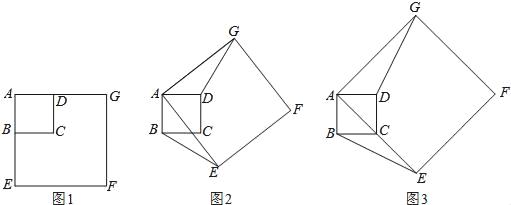
【题目】如图1,正方形ABCD与正方形AEFG的边AB、AE(AB<AE)在一条直线上,正方形AEFG以点A为旋转中心逆时针旋转,设旋转角为α.在旋转过程中,两个正方形只有点A重合,其它顶点均不重合,连接BE、DG.(1)当正方形AEFG旋转至如图2所示的位置时,求证:BE=DG;(2)如图3,如果α=45°,AB=2,AE=4![]() ,求点G到BE的距离.
,求点G到BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
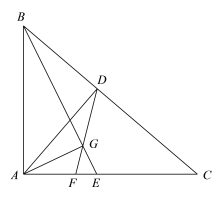
【题目】如图,△ABC中,D是BC上一点,E是AC上一点,点G在BE上,联结DG并延长交AE于点F,∠BGD=∠BAD=∠C.
(1)求证:![]() ;
;
(2)如果∠BAC=90°,求证:AG⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
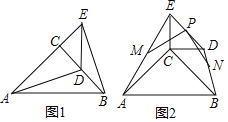
![]() 如图1,点D在BC上,求证:
如图1,点D在BC上,求证:![]() ,
,![]() .
.
![]() 将图1中的
将图1中的![]() 绕点C按逆时针方向旋转到图2所示的位置,旋转角为
绕点C按逆时针方向旋转到图2所示的位置,旋转角为![]() 为锐角
为锐角![]() ,线段DE,AE,BD的中点分别为P,M,N,连接PM,PN.
,线段DE,AE,BD的中点分别为P,M,N,连接PM,PN.
![]() 请直接写出线段PM,PN之间的关系,不需证明;
请直接写出线段PM,PN之间的关系,不需证明;
![]() 若
若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
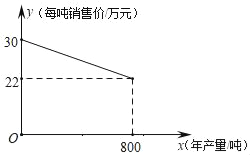
【题目】已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示
(1)当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)
(2)当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】即墨素有“中国针织名城”的美誉,2016年,又被中国服装协会授予“中国童装名称”的称号,该区一网店销售某款童装,当每件售价80元时,每周可卖200件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖20件.已知该款童装每件成本价60元,设该款童装每件售价x(60≤x≤80)元,每周的销售量为y件.
(1)求y与x之间的函数关系式;
(2)设每周的销售利润为W元,当每件售价定为多少元时,每周的销售利润最大,最大利润多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com