
【题目】D为等腰Rt△ABC斜边AB的中点,DM⊥DN,DM,DN分别交BC,CA于点E,F.
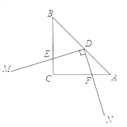
(1)当∠MDN绕点D转动时,求证:DE=DF.
(2)若AB=2,求四边形DECF的面积.
【答案】(1)证明见解析.(2)![]() 。
。
【解析】分析:(1)连CD,根据等腰直角三角形的性质得到CD平分∠ACB,CD⊥AB,∠A=45°,CD=DA,则∠BCD=45°,∠CDA=90°,由DM⊥DN得∠EDF=90°,根据等角的余角相等得到∠CDE=∠ADF,根据全等三角形的判定易得△DCE≌△ADF,即可得到结论;(2)由△DCE≌△ADF,则S△DCE=S△ADF,于是四边形DECF的面积=S△ACD,由而AB=2可得CD=DA=1,根据三角形的面积公式易求得S△ACD,从而得到四边形DECF的面积.
本题解析:
(1)连CD,如图,
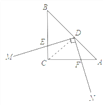
∵D为等腰Rt△ABC斜边AB的中点,
∴CD平分∠ACB,CD⊥AB,∠A=45°,CD=DA,
∴∠BCD=45°,∠CDA=90°,
∵DM⊥DN,
∴∠EDF=90°,
∴∠CDE=∠ADF,
在△DCE和△ADF中,
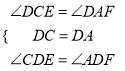 ,
,
∴△DCE≌△ADF(ASA),
∴DE=DF;
(2)∵△DCE≌△ADF,
∴S△DCE=S△ADF,
∴四边形DECF的面积=S△ACD,
而AB=2,
∴CD=DA=1,
∴四边形DECF的面积=S△ACD=![]() CDDA=
CDDA=![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】在甲,乙两个不透明口袋中各装有10个和3个形状大小完全相同的红色小球,则从中摸到红色小球的概率是P甲_____P乙(填“>”,“<”或“=”);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
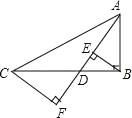
A.不变 B.增大 C.减小 D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
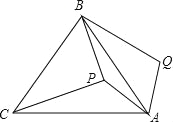
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.能够完全重合的三角形是全等三角形B.面积相等的三角形是全等三角形
C.周长相等的三角形是全等三角形D.所有的等边三角形都是全等三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com