
【题目】如图,已知直线y= ![]() x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 .
x﹣3与x轴、y轴分别交于A、B两点,P在以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB,则△PAB面积的最大值是 . 
【答案】![]()
【解析】过C作CD⊥AB于D,延长DC交⊙C于点P′,此时△P′AB的面积最大,如图所示:
∵直线y=![]() x﹣3与x轴、y轴分别交于A、B两点,
x﹣3与x轴、y轴分别交于A、B两点,
当x=0时,y=-3;当y=0时,x=4,
∴B(0,-3),A(4,0),
∴BO=3,AO=4,
∴AB=![]() =5,
=5,
∵C(0,1),
∴BC=1-(-3)=4,
又∵∠ABO=∠DBC,∠AOB=∠CDB=90°,
∴△AOB∽△CDB,
∴![]() =
=![]() ,
,
∴CD=![]() ,
,
∵⊙C半径为1,
∴P′C=1,
∴P′D=P′C+CD=1+![]() =
=![]() ,
,
∴S△P′AB=![]() ·AB·P′D=
·AB·P′D=![]() ×5×
×5×![]() =
=![]() .
.
故答案为:![]() .
.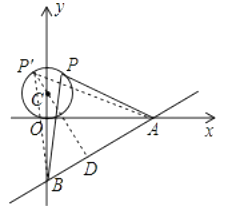
过C作CD⊥AB于D,延长DC交⊙C于点P′,此时△P′AB的面积最大;根据直线解析式得B(0,-3),A(4,0),由勾股定理得AB=5,
根据B、C坐标得BC=4,再由相似三角形判定得△AOB∽△CDB,根据相似三角形性质得![]() =
=![]() ,代入数值得CD=
,代入数值得CD=![]() ,由已知得P′C=1,
,由已知得P′C=1,
再由P′D=P′C+CD=![]() ,根据三角形面积公式得S△P′AB=
,根据三角形面积公式得S△P′AB=![]() ·AB·P′D=
·AB·P′D=![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.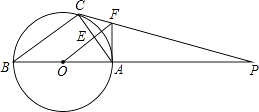
(1)判断AF与⊙O的位置关系并说明理由;
(2)已知半径为20,AF=15,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax ![]() +bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①
+bx+c经过点(-1,0),对称轴l如图所示.则下列结论:①
abc >0;②a-b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )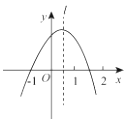
A.①③
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在等腰△ABC 中,AB=AC=10,BC=16.
(1)若将△ABC 的腰不变,底变为 12,甲同学说,这两个等腰三角形面积相等;乙同学说,腰不变,底变化,这两个三角形面积必不相等,请对甲、乙两种说法做出判断,并说明理由;
(2)已知△ABC 底边上高增加 x,腰长增加(x﹣2)时,底却保持不变,请确定 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在公园道一号购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:

(1)用含x的代数式表示地面总面积
(2)当x=3时,若铺1m2地砖的平均费用为100元, 那么王老师要将全部地面铺地砖,总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
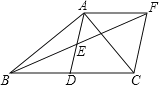
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF.
(1) 求证:AD=AF;
(2) 当△ABC满足什么条件时,四边形ADCF是矩形.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形AB1C1D1的边长为1,∠B1=60°;作AD2⊥B1C1于点D2 , 以AD2为一边,做第二个菱形AB2C2D2 , 使∠B2=60°;作AD3⊥B2C2于点D3 , 以AD3为一边做第三个菱形AB3C3D3 , 使∠B3=60°…依此类推,这样做的第n个菱形ABnCnDn的边ADn的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+2x+3与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C.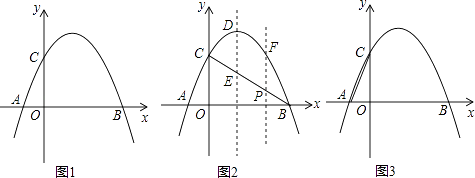
(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)如图2,连接BC,与抛物线的对称轴交于点E,点P位线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;用含m的代数式表示线段PF的长;并求出当m为何值时,四边形PEDF为平行四边形?
(3)如图3,连接AC,在x轴上是否存在点Q,使△ACQ为等腰三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com