
【题目】.根据图5中①所示的程序,得到了y与x的函数图象,如图5中②,若点M是
y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,连接OP、OQ,则以下结论:
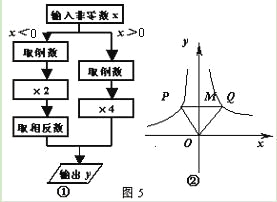
①x<0时,y=![]()
②△OPQ的面积为定值
③x>0时,y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确结论是
A.①②④B.②④⑤C.③④⑤D.②③⑤
【答案】B
【解析】
由流程图可知函数解析式从而判断①;S△OPQ= S△PMQ+ S△MQO=1+2=3,可判断②;由图像可判断③;由流程图可知函数解析式:x<0时,y=![]() ;x>0时,y=
;x>0时,y=![]() ,再分别用OM表示PM和MQ即可证明;∠POQ=90°时,△PMO∽△OMQ,利用相似的性质可求解出PM、QM以及OM三者之间的关系,即PM、QM以及OM三者之间满足一定的数量关系可得到∠POQ=90°,据此判断⑤.
,再分别用OM表示PM和MQ即可证明;∠POQ=90°时,△PMO∽△OMQ,利用相似的性质可求解出PM、QM以及OM三者之间的关系,即PM、QM以及OM三者之间满足一定的数量关系可得到∠POQ=90°,据此判断⑤.
解:由流程图可知,x<0时,y=![]() ,故①错误;由反比例函数系数k的几何意义可得S△PMQ =1,S△MQO=2,则S△OPQ= S△PMQ+ S△MQO=1+2=3,故②正确;由图像可知,x>0时,y随x的增大而减小,故③错误;由流程图可知函数解析式:x<0时,y=
,故①错误;由反比例函数系数k的几何意义可得S△PMQ =1,S△MQO=2,则S△OPQ= S△PMQ+ S△MQO=1+2=3,故②正确;由图像可知,x>0时,y随x的增大而减小,故③错误;由流程图可知函数解析式:x<0时,y=![]() ;x>0时,y=
;x>0时,y=![]() ,则PM=
,则PM=![]() ,MQ=
,MQ=![]() ,则MQ=2PM,故④正确;∠POQ=90°时,△PMO∽△OMQ,则
,则MQ=2PM,故④正确;∠POQ=90°时,△PMO∽△OMQ,则![]() ,则可得OM2=PM×MQ,即当OM2=PM×MQ时,∠POQ=90°,故⑤正确.
,则可得OM2=PM×MQ,即当OM2=PM×MQ时,∠POQ=90°,故⑤正确.
故选择D.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )
A. AB=c,AC=b,BC=a,DE=![]() ,EF=
,EF=![]() ,DF=
,DF=![]()
B. AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1
C. AB=3,AC=4,BC=6,DE=12,EF=8,DF=6
D. AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,DE=
,DE=![]() ,EF=3,DF=3
,EF=3,DF=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y=![]() x向上平移4个单位长度后,与y轴交于点C,与双曲线y=
x向上平移4个单位长度后,与y轴交于点C,与双曲线y=![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
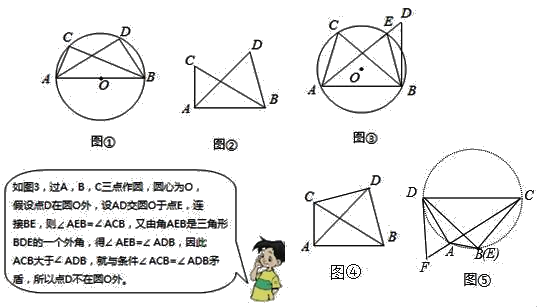
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的计算器,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是600个,而销售单价每上涨1元,就会少售出10个.
(1)不妨设该种品牌计算器的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(个) |
|
销售计算器获得利润w(元) |
|
(2)在第(1)问的条件下,若计算器厂规定该品牌计算器销售单价不低于35元,且商场要完成不少于500个的销售任务,求:商场销售该品牌计算器获得最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com