
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
【答案】发现:点D也不在⊙O内;证明见解析;应用:(1)40°;(2)![]() .
.
【解析】
发现:如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上.如图⑤中,点假设D在⊙O内,延长AD交△ABC的外接圆于E,连接BE.利用反证法即可解决问题;
应用:(1)只要证明A、B、C、D四点共圆即可解决问题;
(2)只要证明点E与B重合,由∠DBC=∠DAC=90°,CD=3,BC=2,推出DE=DB=![]() =
=![]() .
.
解:发现:如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上.
如图⑤中,点假设D在⊙O内,延长AD交△ABC的外接圆于E,连接BE.
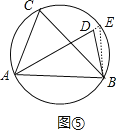
∵∠ACB=∠AEB,∠ADB>∠AEB,
∴∠ADB>∠ACB,这个与已知条件∠ACB=∠ADB矛盾,
∴假设不成立,
∴点D也不在⊙O内.
应用(1)如图④中,
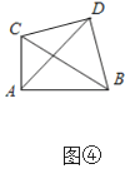
∵∠DCB=∠DAB,
∴A、B、C、D四点共圆,
∴∠CBD=∠CAD=40°,
(2)如图⑤中,

∵∠CDF=∠DAC=90°,
∴∠ADF+∠CDA=90°,∠CDA+∠ACD=90°,
∴∠ADF=∠ACD,
∵∠ADF=∠AED,
∴∠AED=∠ACD,
∵∠ACD=∠ABD,
∴点E与B重合,
∵∠DBC=∠DAC=90°,CD=3,BC=2,
∴DE=DB=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为12,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C处,P为直线AD上的一点,则线段BP的长可能是( )
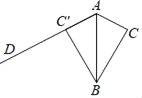
A. 3 B. 5 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化简,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是![]() 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.
(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.
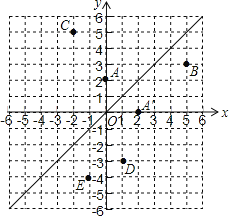
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:![]() ___________、
___________、![]() ___________;
___________;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为___________(不必证明);
的坐标为___________(不必证明);
(3)已知两点![]() 、
、![]() ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
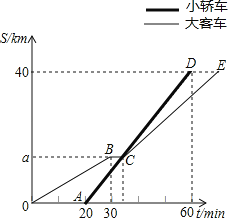
【题目】某班同学从学校出发去太阳岛春游,大部分同学乘坐大客车先出发,余下的同学乘坐小轿车20分钟后出发,沿同一路线行驶.大客车中途停车等候5分钟,小轿车赶上来之后,大客车以原速度的![]() 继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
①学校到景点的路程为40km;
②小轿车的速度是1km/min;
③a=15;
④当小轿车驶到景点入口时,大客车还需要10分钟才能到达景点入口.
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com