
【题目】如图,△ABC的面积为12,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C处,P为直线AD上的一点,则线段BP的长可能是( )
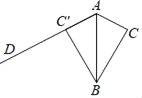
A. 3 B. 5 C. 6 D. 10
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
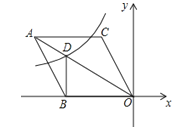
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查今年有多少名学生参加中考,小明从全市所有家庭中随机抽查了200个家庭,发现其中有10个家庭有子女参加中考。
(1)本次抽查的200个家庭中,有子女参加中考的家庭的频率是多少?
(2)如果你随机调查一个家庭,估计该家庭有子女参加中考的概率是多少?
(3)已知全市约有1.3×106个家庭,假设有子女参加中考的每个家庭中只有一名考生,请你估计今年全市有多少名考生参加中考?
查看答案和解析>>
科目:初中数学 来源: 题型:
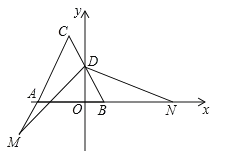
【题目】已知:等边三角形![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() .
.
(1)如图,求![]() 、
、![]() 的坐标及
的坐标及![]() 的长;
的长;
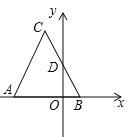
(2)如图,点![]() 是
是![]() 延长线上一点,点
延长线上一点,点![]() 是
是![]() 右侧一点,
右侧一点,![]() ,且
,且![]() .连接
.连接![]() .
.
求证:直线![]() 必过点
必过点![]() 关于
关于![]() 轴对称的对称点;
轴对称的对称点;
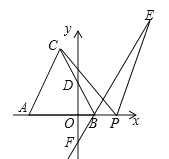
(3)如图,若点![]() 在
在![]() 延长线上,点
延长线上,点![]() 在
在![]() 延长线上,且
延长线上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)
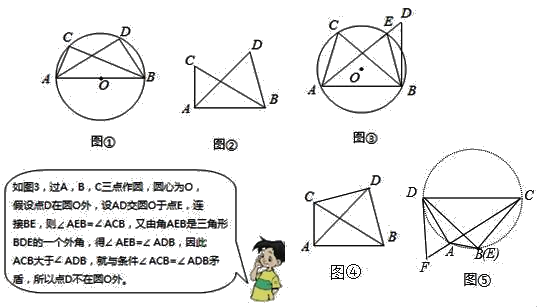
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com