
【题目】某班同学从学校出发去太阳岛春游,大部分同学乘坐大客车先出发,余下的同学乘坐小轿车20分钟后出发,沿同一路线行驶.大客车中途停车等候5分钟,小轿车赶上来之后,大客车以原速度的![]() 继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
①学校到景点的路程为40km;
②小轿车的速度是1km/min;
③a=15;
④当小轿车驶到景点入口时,大客车还需要10分钟才能到达景点入口.
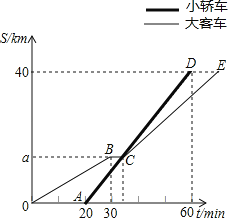
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
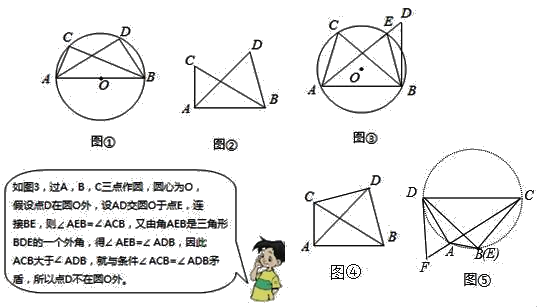
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
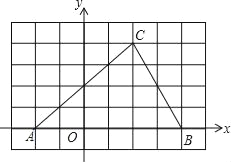
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
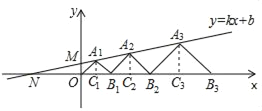
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+
x+![]() 和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(
和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(![]() ,
,![]() ),那么点A3的纵坐标是( )
),那么点A3的纵坐标是( )
A. ![]() B. 2cm C.
B. 2cm C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.
(1)证明:△ABM∽△MCN;
(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
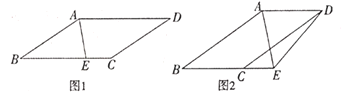
【题目】如图,已知∠ABC=∠ADC,AB∥CD,E为射线BC上一点,AE平分∠BAD.
(1)如图1,当点E在线段BC上时,求证:∠BAE=∠BEA.
(2)如图2,当点E在线段BC延长线上时,连接DE,若∠ADE=3∠CDE,∠AED=60°,求∠CED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
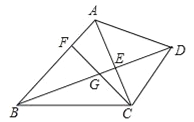
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
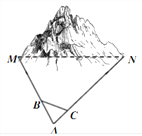
【题目】中国高铁近年来用震惊世界的速度不断发展,已成为当代中国一张耀眼的“国家名片”。修建高铁时常常要逢山开道、遇水搭桥。如图,某高铁在修建时需打通一直线隧道MN(M、N为山的两侧),工程人员为了计算MN两点之间的直线距离,选择了在测量点A、B、C进行测量,点B、C分别在AM、AN上,现测得AM=1200米,AN=2000米,AB=30米,BC=45米,AC=18米,求直线隧道MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为半圆O的直径,C是半圆O上一点,过点C作AB的平行线交⊙O于点E,连接AC、BC、AE,EB. 过点C作CG⊥AB于点G,交EB于点H.
(1)求证:∠BCG=∠EBG;
(2)若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com