
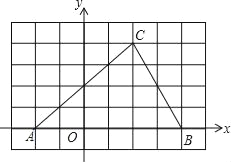
【题目】如图,在6×8的网格图中,每个小正方形边长均为1,原点O和△ABC的顶点均为格点.
(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′与△ABC位似,且位似比为1:2;(保留作图痕迹,不要求写作法和证明)
(2)若点C的坐标为(2,4),则点A′的坐标为( , ),点C′的坐标为( , ),S△A′B′C′:S△ABC= .
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化简,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个实数,规定a与b之间的一种运算“⊕”为:a⊕b= ,
,
例如:1⊕(﹣3)=![]() =﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
=﹣3,(﹣3)⊕2=(﹣3)﹣2 =﹣5,
(x2+1)⊕(x﹣1)=![]() (因为x2+1>0)
(因为x2+1>0)
参照上面材料,解答下列问题:
(1)2⊕4= ,(﹣2)⊕4= ;
(2)若x>![]() ,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
,且满足(2x﹣1)⊕(4x2﹣1)=(﹣4)⊕(1﹣4x),求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.
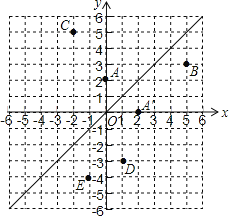
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:![]() ___________、
___________、![]() ___________;
___________;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为___________(不必证明);
的坐标为___________(不必证明);
(3)已知两点![]() 、
、![]() ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
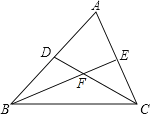
【题目】如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
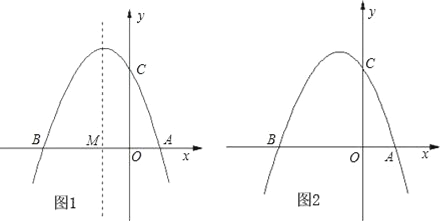
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学从学校出发去太阳岛春游,大部分同学乘坐大客车先出发,余下的同学乘坐小轿车20分钟后出发,沿同一路线行驶.大客车中途停车等候5分钟,小轿车赶上来之后,大客车以原速度的![]() 继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
继续行驶,小轿车保持速度不变.两车距学校的路程S(单位:km)和大客车行驶的时间t(单位:min)之间的函数关系如图所示.下列说法中正确的个数是( )
①学校到景点的路程为40km;
②小轿车的速度是1km/min;
③a=15;
④当小轿车驶到景点入口时,大客车还需要10分钟才能到达景点入口.
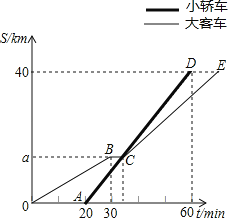
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
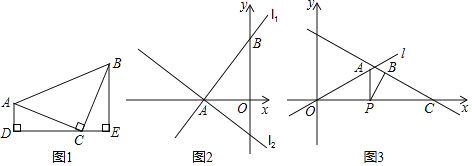
【题目】(模型建立)
(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△CDA≌△BEC.
(模型运用)
(2)如图2,直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,求直线l2的函数表达式.
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转90°至直线l2,求直线l2的函数表达式.
(模型迁移)
如图3,直线l经过坐标原点O,且与x轴正半轴的夹角为30°,点A在直线l上,点P为x轴上一动点,连接AP,将线段AP绕点P顺时针旋转30°得到BP,过点B的直线BC交x轴于点C,∠OCB=30°,点B到x轴的距离为2,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com