
如图,在△ABC中,E、F分别是AB、AC的中点,△CEF的面积为2.5,则△ABC的面积为__________.

10.
【考点】三角形的面积.
【分析】由于E、F分别是AB、AC的中点,可知EF是△ABC的中位线,利用中位线的性质可知EF∥BC,且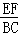 =
=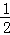 ,根据△AEF和△CEF是同底等高,△BCE和△CEF是同高,求得△AEF的面积为2.5,△BCE的面积为2.5×2=5,进而求得∴△ABC的面积等于10.
,根据△AEF和△CEF是同底等高,△BCE和△CEF是同高,求得△AEF的面积为2.5,△BCE的面积为2.5×2=5,进而求得∴△ABC的面积等于10.
【解答】解:∵E、F分别是AB、AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,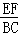 =
=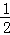 ,
,
∵△CEF的面积为2.5,
∵△AEF和△CEF是同底等高,△BCE和△CEF是同高,
∴△AEF的面积为2.5,△BCE的面积为2.5×2=5,
∴△ABC的面积等于10.
故答案为10.
【点评】本题考查了中位线的判定和性质以及三角形面积,求得△AEF和△CEF,△BCE和△CEF的关系是解题的关键.


科目:初中数学 来源: 题型:
把抛物线y=x2向左平移1个单位,所得的新抛物线的函数表达式为( )
A.y=x2+1 B.y=(x+1)2 C.y=x2﹣1 D.y=(x﹣1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠ABC=∠ACB, AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14 ,则BC的长为 .
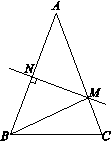
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
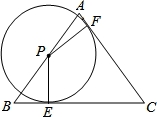
A.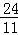 B.2 C.
B.2 C.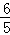 D.
D.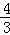
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,已知二次函数y=ax2﹣8ax+12(a>0)的图象与x轴分别交于A、B两点,与y轴交于点C,点P在抛物线的对称轴上,且四边形ABPC为平行四边形.
(1)求此抛物线的对称轴,并确定此二次函数的解析式;
(2)点M为x轴下方抛物线上一点,若△OMP的面积为36,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com