
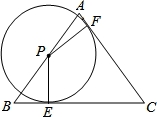
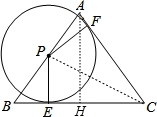
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
A.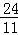 B.2 C.
B.2 C.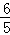 D.
D.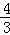
A【考点】切线的性质.
【专题】计算题.
【分析】连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,根据等腰三角形的性质得BH=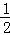 BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到
BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到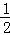 BC×AH=
BC×AH=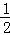 BC×PE+
BC×PE+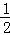 AC×PF,即6×4=6r+5r,然后解方程即可.
AC×PF,即6×4=6r+5r,然后解方程即可.
【解答】解:连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,
∵AB=AC=5,
∴BH=CH=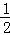 BC=3,
BC=3,
∴AH=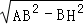 =4,
=4,
∵以P为圆心的⊙P分别与边AC、BC相切于点E、F,
∴PE⊥BC,PF⊥AC,
∵S△ABC=S△PAC+S△PBC,
∴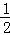 BC×AH=
BC×AH=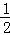 BC×PE+
BC×PE+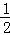 AC×PF,
AC×PF,
即6×4=6r+5r,
∴r=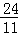 .
.
故选A.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰三角形的性质和三角形面积公式.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
父亲节,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
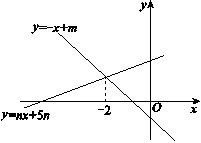
如图,直线y=﹣x+m与直线y=nx+5n(n≠0)的交点的横坐标为
﹣2,则关于x的不等式﹣x+m>nx+5n>0的整数解为( ).
A.﹣5 ,﹣4,﹣3 B. ﹣4,﹣3
C.﹣4 ,﹣3,﹣2 D. ﹣3,﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系xOy中,将正比例函数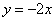 的图象沿
的图象沿 轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
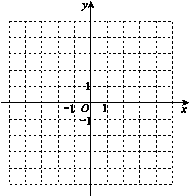
(1)画正比例函数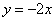 的图象,并直接写出直线BC的解析式;
的图象,并直接写出直线BC的解析式;
(2)如果一条直线经过点C且与正比例函数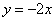 的图象交于点P(m,2),求m的值及直线
的图象交于点P(m,2),求m的值及直线
查看答案和解析>>
科目:初中数学 来源: 题型:
九年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学答题比赛,共10题,答对题数统计如表一:
(表一)
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
(表二)
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
(1)根据表一中统计的数据,完成表二;
(2)请你从平均数和方差的角度分析,哪组的成绩更好些?
查看答案和解析>>
科目:初中数学 来源: 题型:
题面:如图,在△ABC中,∠ABC和∠A CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
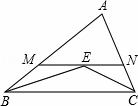
A.6 B.7 C.8 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com