练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：（﹣1）1+（﹣1）2+（﹣1）3+…+（﹣1）2016=

    【答案】0
    【解析】解：（﹣1）1+（﹣1）2+（﹣1）3+…+（﹣1）2016=﹣1+1+（﹣1）+1+…+1
    =0，
    所以答案是：0．
    【考点精析】本题主要考查了有理数的四则混合运算的相关知识点，需要掌握在没有括号的不同级运算中，先算乘方再算乘除，最后算加减才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

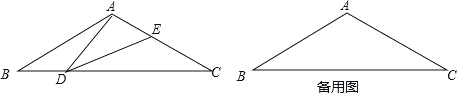
    【题目】如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．

    （1）求证：△ABD∽△DCE；

    （2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；

    （3）当△ADE是等腰三角形时，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某区10名学生参加实际汉字听写大赛，他们得分情况如表：那么10名学生所得分数的中位数是_____．

    人数

    3

    4

    2

    1

    分数

    80

    85

    90

    95

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A.过一点有且只有一条直线与已知直线平行

    B.同旁内角互补

    C.点到直线的距离就是这点到这条直线所作的垂线段

    D.实数与数轴上的点一一对应

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中，正确的是（ ）

    A.x3·x3=x6B.3x2+2x3=5x5C.(x2)3=x5D.(x+y2)2=x2+y4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题。下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．

    探究一：求不等式的解集

    （1）探究的几何意义

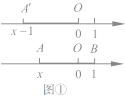
    如图①，在以O为原点的数轴上，设点A＇对应点的数为，由绝对值的定义可知，点A＇与O的距离为，

    可记为：A＇O=。将线段A＇O向右平移一个单位，得到线段AB，，此时点A对应的数为，点B的对应数是1，

    因为AB= A＇O，所以AB=。

    因此，的几何意义可以理解为数轴上所对应的点A与1所对应的点B之间的距离AB。

    （2）求方程=2的解

    因为数轴上3与所对应的点与1所对应的点之间的距离都为2，所以方程的解为

    （3）求不等式的解集

    因为表示数轴上所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点所对应的数的范围。

    请在图②的数轴上表示的解集，并写出这个解集

    探究二：探究的几何意义

    （1）探究的几何意义

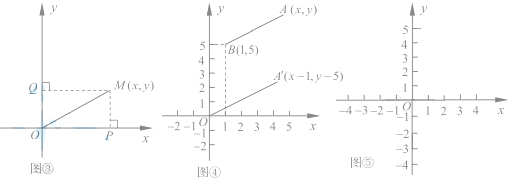
    如图③，在直角坐标系中，设点M的坐标为，过M作MP⊥x轴于P，作MQ⊥y轴于Q，则点P点坐标（），Q点坐标（），|OP|=，|OQ|=，

    在Rt△OPM中，PM＝OQ＝y，则

    因此的几何意义可以理解为点M与原点O（0,0）之间的距离OM

    （2）探究的几何意义

    如图④，在直角坐标系中，设点 A＇的坐标为，由探究（二）（1）可知，

    A＇O=，将线段 A＇O先向右平移1个单位，再向上平移5个单位，得到线段AB，此时A的坐标为（），点B的坐标为（1,5）。

    因为AB= A＇O，所以 AB=，因此的几何意义可以理解为点A（）与点B（1,5）之间的距离。

    （3）探究的几何意义

    请仿照探究二（2）的方法，在图⑤中画出图形，并写出探究过程。

    （4）的几何意义可以理解为：_________________________.

    拓展应用：

    （1）+的几何意义可以理解为：点A与点E的距离与点AA与点F____________（填写坐标）的距离之和。

    （2）+的最小值为____________(直接写出结果)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若定义：f(a,b)＝(-a,b)，g(m,n)＝(m,-n)，例如f(1,2)＝(-1,2)，g(-4,-5)＝(-4,5)，则g(f(3,-4))的值为（ ）

    A.(3,-4)B.(-3,4)C.(3,4)D.(-3,-4)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知三边作三角形，用到的基本作图是（ ）

    A. 作一个角等于已知角 B. 平分一个已知角

    C. 在射线上截取一线段等于已知线段 D. 作一条直线的垂线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（　　）

    A.a3a2＝a6B.a7÷a3＝a4

    C.（﹣3a）2 ＝﹣6a2D.（a﹣1）2＝a2﹣1

    查看答案和解析>>

    同步练习册答案