
ЁОЬтФПЁПЪ§КЭаЮЪЧЪ§бЇЕФСНИіжївЊбаОПЖдЯѓЃЌЮвУЧОГЃдЫгУЪ§аЮНсКЯЁЂЪ§аЮзЊЛЏЕФЗНЗЈНтОівЛаЉЪ§бЇЮЪЬтЁЃЯТУцЮвУЧРДЬНОПЁАгЩЪ§ЫМаЮЃЌвдаЮжњЪ§ЁБЕФЗНЗЈдкНтОіДњЪ§ЮЪЬтжаЕФгІгУЃЎ
ЬНОПвЛЃКЧѓВЛЕШЪН![]() ЕФНтМЏ
ЕФНтМЏ
ЃЈ1ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
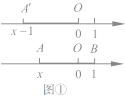
ШчЭМЂйЃЌдквдOЮЊдЕуЕФЪ§жсЩЯЃЌЩшЕуAЃЇЖдгІЕуЕФЪ§ЮЊ![]() ЃЌгЩОјЖджЕЕФЖЈвхПЩжЊЃЌЕуAЃЇгыOЕФОрРыЮЊ
ЃЌгЩОјЖджЕЕФЖЈвхПЩжЊЃЌЕуAЃЇгыOЕФОрРыЮЊ![]() ЃЌ
ЃЌ
ПЩМЧЮЊЃКAЃЇO=![]() ЁЃНЋЯпЖЮAЃЇOЯђгвЦНвЦвЛИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌЃЌДЫЪБЕуAЖдгІЕФЪ§ЮЊ
ЁЃНЋЯпЖЮAЃЇOЯђгвЦНвЦвЛИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌЃЌДЫЪБЕуAЖдгІЕФЪ§ЮЊ![]() ЃЌЕуBЕФЖдгІЪ§ЪЧ1ЃЌ
ЃЌЕуBЕФЖдгІЪ§ЪЧ1ЃЌ
вђЮЊAB= AЃЇOЃЌЫљвдAB=![]() ЁЃ
ЁЃ
вђДЫЃЌ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЪ§жсЩЯ
ЕФМИКЮвтвхПЩвдРэНтЮЊЪ§жсЩЯ![]() ЫљЖдгІЕФЕуAгы1ЫљЖдгІЕФЕуBжЎМфЕФОрРыABЁЃ
ЫљЖдгІЕФЕуAгы1ЫљЖдгІЕФЕуBжЎМфЕФОрРыABЁЃ
ЃЈ2ЃЉЧѓЗНГЬ![]() =2ЕФНт
=2ЕФНт
вђЮЊЪ§жсЩЯ3гы![]() ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЖМЮЊ2ЃЌЫљвдЗНГЬЕФНтЮЊ
ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЖМЮЊ2ЃЌЫљвдЗНГЬЕФНтЮЊ![]()
ЃЈ3ЃЉЧѓВЛЕШЪН![]() ЕФНтМЏ
ЕФНтМЏ
вђЮЊ![]() БэЪОЪ§жсЩЯ
БэЪОЪ§жсЩЯ![]() ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЃЌЫљвдЧѓВЛЕШЪННтМЏОЭзЊЛЏЮЊЧѓетИіОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§
ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЃЌЫљвдЧѓВЛЕШЪННтМЏОЭзЊЛЏЮЊЧѓетИіОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§![]() ЕФЗЖЮЇЁЃ
ЕФЗЖЮЇЁЃ
ЧыдкЭМЂкЕФЪ§жсЩЯБэЪО![]() ЕФНтМЏЃЌВЂаДГіетИіНтМЏ
ЕФНтМЏЃЌВЂаДГіетИіНтМЏ
![]()
ЬНОПЖўЃКЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ЃЈ1ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
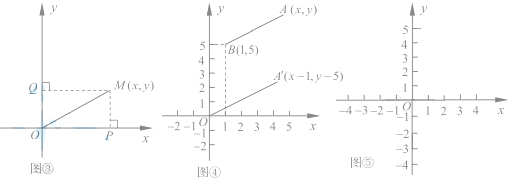
ШчЭМЂлЃЌдкжБНЧзјБъЯЕжаЃЌЩшЕуMЕФзјБъЮЊ![]() ЃЌЙ§MзїMPЁЭxжсгкPЃЌзїMQЁЭyжсгкQЃЌдђЕуPЕузјБъЃЈ
ЃЌЙ§MзїMPЁЭxжсгкPЃЌзїMQЁЭyжсгкQЃЌдђЕуPЕузјБъЃЈ![]() ЃЉЃЌQЕузјБъЃЈ
ЃЉЃЌQЕузјБъЃЈ![]() ЃЉЃЌ|OP|=
ЃЉЃЌ|OP|=![]() ЃЌ|OQ|=
ЃЌ|OQ|=![]() ЃЌ
ЃЌ
дкRtЁїOPMжаЃЌPMЃНOQЃНyЃЌдђ![]()
вђДЫ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуM
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуM![]() гыдЕуOЃЈ0,0ЃЉжЎМфЕФОрРыOM
гыдЕуOЃЈ0,0ЃЉжЎМфЕФОрРыOM
ЃЈ2ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ШчЭМЂмЃЌдкжБНЧзјБъЯЕжаЃЌЩшЕу AЃЇЕФзјБъЮЊ![]() ЃЌгЩЬНОПЃЈЖўЃЉЃЈ1ЃЉПЩжЊЃЌ
ЃЌгЩЬНОПЃЈЖўЃЉЃЈ1ЃЉПЩжЊЃЌ
AЃЇO=![]() ЃЌНЋЯпЖЮ AЃЇOЯШЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ5ИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌДЫЪБAЕФзјБъЮЊЃЈ
ЃЌНЋЯпЖЮ AЃЇOЯШЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ5ИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌДЫЪБAЕФзјБъЮЊЃЈ![]() ЃЉЃЌЕуBЕФзјБъЮЊЃЈ1,5ЃЉЁЃ
ЃЉЃЌЕуBЕФзјБъЮЊЃЈ1,5ЃЉЁЃ
вђЮЊAB= AЃЇOЃЌЫљвд AB=![]() ЃЌвђДЫ
ЃЌвђДЫ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ![]() ЃЉгыЕуBЃЈ1,5ЃЉжЎМфЕФОрРыЁЃ
ЃЉгыЕуBЃЈ1,5ЃЉжЎМфЕФОрРыЁЃ
ЃЈ3ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ЧыЗТееЬНОПЖўЃЈ2ЃЉЕФЗНЗЈЃЌдкЭМЂнжаЛГіЭМаЮЃЌВЂаДГіЬНОПЙ§ГЬЁЃ
ЃЈ4ЃЉ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЃК_________________________.
ЕФМИКЮвтвхПЩвдРэНтЮЊЃК_________________________.
ЭиеЙгІгУЃК
ЃЈ1ЃЉ![]() +
+![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЃКЕуA
ЕФМИКЮвтвхПЩвдРэНтЮЊЃКЕуA![]() гыЕуE
гыЕуE![]() ЕФОрРыгыЕуAA
ЕФОрРыгыЕуAA![]() гыЕуF____________ЃЈЬюаДзјБъЃЉЕФОрРыжЎКЭЁЃ
гыЕуF____________ЃЈЬюаДзјБъЃЉЕФОрРыжЎКЭЁЃ
ЃЈ2ЃЉ![]() +
+![]() ЕФзюаЁжЕЮЊ____________(жБНгаДГіНсЙћ)
ЕФзюаЁжЕЮЊ____________(жБНгаДГіНсЙћ)
ЁОД№АИЁПЬНОПвЛЃЈ3ЃЉ 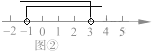 НтМЏЮЊЃК
НтМЏЮЊЃК![]()
ЬНОПЖўЃЈ3ЃЉЃЈ![]() ЃЉЭиеЙгІгУЃЈ1ЃЉЃЈ
ЃЉЭиеЙгІгУЃЈ1ЃЉЃЈ![]() ЃЉ ЃЈ2ЃЉ5
ЃЉ ЃЈ2ЃЉ5
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЬНОПвЛЃЈ3ЃЉЃК![]() ЕФНтМЏОЭЪЧЪ§жсЩЯ
ЕФНтМЏОЭЪЧЪ§жсЩЯ![]() ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§ЃЌРћгУЪ§жсПЩжЊ
ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§ЃЌРћгУЪ§жсПЩжЊ![]()
ЬНОПЖўЃЈ3ЃЉЃКИљОнЬтФПаХЯЂЃЌ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ![]() ЃЉгыЕуBЃЈ
ЃЉгыЕуBЃЈ![]() ЃЉжЎМфЕФОрРыЁЃ
ЃЉжЎМфЕФОрРыЁЃ
ЭиеЙгІгУЃКИљОнЬтФПаХЯЂжЊЪЧгыЕуFЃЈ![]() ЃЉЕФОрРыжЎКЭЁЃ
ЃЉЕФОрРыжЎКЭЁЃ
![]() +
+![]() БэЪОЕуA
БэЪОЕуA![]() гыЕуE
гыЕуE![]() ЕФОрРыгыЕуA
ЕФОрРыгыЕуA![]() гыЕуFЃЈ
гыЕуFЃЈ![]() ЃЉЕФОрРыжЎКЭЁЃЁрзюаЁжЕЮЊE
ЃЉЕФОрРыжЎКЭЁЃЁрзюаЁжЕЮЊE![]() гыЕуFЃЈ
гыЕуFЃЈ![]() ЃЉЕФОрРы5.
ЃЉЕФОрРы5.
ЪдЬтНтЮіЃКЬНОПвЛ
ЃЈ3ЃЉ 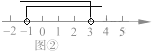
НтМЏЮЊЃК![]()
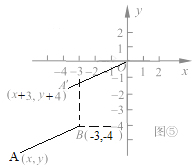
ЬНОПЖўЃЈ3ЃЉ
ШчЭМЂнЃЌдкжБНЧзјБъЯЕжаЃЌЩшЕу AЃЇЕФзјБъЮЊ![]() ЃЌ
ЃЌ
гЩЬНОПЃЈЖўЃЉЃЈ1ЃЉПЩжЊЃЌ AЃЇO=![]() ЃЌ
ЃЌ
НЋЯпЖЮ AЃЇOЯШЯђзѓЦНвЦ3ИіЕЅЮЛЃЌдйЯђЯТЦНвЦ4ИіЕЅЮЛЃЌ
ЕУЕНЯпЖЮABЃЌДЫЪБAЕФзјБъЮЊЃЈ![]() ЃЉЃЌЕуBЕФзјБъЮЊЃЈ
ЃЉЃЌЕуBЕФзјБъЮЊЃЈ![]() ЃЉЁЃ
ЃЉЁЃ
вђЮЊAB= AЃЇOЃЌЫљвд AB=![]() ЃЌ
ЃЌ
вђДЫ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ![]() ЃЉгыЕуBЃЈ
ЃЉгыЕуBЃЈ![]() ЃЉжЎМфЕФОрРыЁЃ
ЃЉжЎМфЕФОрРыЁЃ
ЭиеЙгІгУ
ЃЈ1ЃЉЃЈ![]() ЃЉ ЃЈ2ЃЉ5
ЃЉ ЃЈ2ЃЉ5



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊДѓСІКыбяЁАЗюЯзЁЂгбАЎЁЂЛЅжњЁЂНјВНЁБЕФжОдИЗўЮёОЋЩёЃЌДЋВЅЁАЗюЯзЫћШЫЁЂЬсЩ§здЮвЁБЕФжОдИЗўЮёРэФюЃЌЖЋгЊЪаФГжабЇРћгУжмФЉЪБМфПЊеЙСЫЁАжњРЯжњВаЁЂЩчЧјЗўЮёЁЂЩњЬЌЛЗБЃЁЂЭјТчЮФУїЁБЫФИіжОдИЗўЮёЛюЖЏЃЈУПШЫжЛВЮМгвЛИіЛюЖЏЃЉЃЌОХФъМЖФГАрШЋАрЭЌбЇЖМВЮМгСЫжОдИЗўЮёЃЌАрГЄЮЊСЫНтжОдИЗўЮёЕФЧщПіЃЌЪеМЏећРэЪ§ОнКѓЃЌЛцжЦвдЯТВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓИУАрЕФШЫЪ§ЃЛ
ЃЈ2ЃЉЧыАбелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЧѓЩШаЮЭГМЦЭМжаЃЌЭјТчЮФУїВПЗжЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉаЁУїКЭаЁРіВЮМгСЫжОдИЗўЮёЛюЖЏЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЫћУЧВЮМгЭЌвЛЗўЮёЛюЖЏЕФИХТЪЃЎ
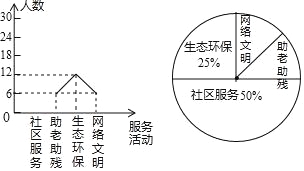
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГаЃбЇЩњЖдЁЖзюЧПДѓФдЁЗЁЂЁЖРЪЖСепЁЗЁЂЁЖжаЙњЪЋДЪДѓЛсЁЗЁЂЁЖГіВЪжаЙњШЫЁЗЫФИіЕчЪгНкФПЕФЯВАЎЧщПіЃЌЫцЛњГщШЁСЫ![]() УћбЇЩњНјааЕїВщЭГМЦЃЈвЊЧѓУПУћбЇЩњбЁГіВЂЧвжЛФмбЁГівЛИіздМКзюЯВАЎЕФНкФПЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТЭГМЦЭМБэЃК
УћбЇЩњНјааЕїВщЭГМЦЃЈвЊЧѓУПУћбЇЩњбЁГіВЂЧвжЛФмбЁГівЛИіздМКзюЯВАЎЕФНкФПЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТЭГМЦЭМБэЃК
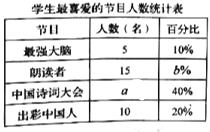

ИљОнвдЩЯЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ______ЃЌ
______ЃЌ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
ЃЈ2ЃЉВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ1000Ућ.ИљОнГщбљЕїВщНсЙћЃЌЙРМЦИУаЃзюЯВАЎЁЖжаЙњЪЋДЪДѓЛсЁЗНкФПЕФбЇЩњгаЖрЩйУћ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃКЃЈЉ1ЃЉ1+ЃЈЉ1ЃЉ2+ЃЈЉ1ЃЉ3+Ё+ЃЈЉ1ЃЉ2016=
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзБШввДѓ15ЫъЃЌ5ФъЧАМзЕФФъСфЪЧввЕФФъСфЕФСНБЖЃЌввЯждкЕФФъСфЪЧ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЎ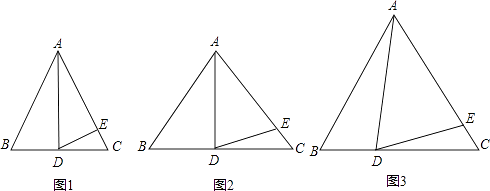
ЃЈ1ЃЉШчЭМ1ЃЌШчЙћЁЯBAD=30ЁуЃЌADЪЧBCЩЯЕФИпЃЌAD=AEЃЌдђЁЯEDC=
ЃЈ2ЃЉШчЭМ2ЃЌШчЙћЁЯBAD=40ЁуЃЌADЪЧBCЩЯЕФИпЃЌAD=AEЃЌдђЁЯEDC=
ЃЈ3ЃЉЫМПМЃКЭЈЙ§вдЩЯСНЬтЃЌФуЗЂЯжЁЯBADгыЁЯEDCжЎМфгаЪВУДЙиЯЕЃПЧыгУЪНзгБэЪОЃК
ЃЈ4ЃЉШчЭМ3ЃЌШчЙћADВЛЪЧBCЩЯЕФИпЃЌAD=AEЃЌЪЧЗёШдгаЩЯЪіЙиЯЕЃПШчгаЃЌЧыФуаДГіРДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСавЛзщЪЧАДЙцТЩХХСаЕФЪ§ЃК1ЃЌ2ЃЌ4ЃЌ8ЃЌ16ЃЌЁЃЌЕк2016ИіЪ§ЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌБпABЁЂACЕФДЙжБЦНЗжЯпЗжБ№НЛБпBCгкЕуDЁЂE,ШєЁЯDAE=40ЁуЃЌдђЁЯBACЕФЖШЪ§ЮЊ________________.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com