
ЁОЬтФПЁПЮЊДѓСІКыбяЁАЗюЯзЁЂгбАЎЁЂЛЅжњЁЂНјВНЁБЕФжОдИЗўЮёОЋЩёЃЌДЋВЅЁАЗюЯзЫћШЫЁЂЬсЩ§здЮвЁБЕФжОдИЗўЮёРэФюЃЌЖЋгЊЪаФГжабЇРћгУжмФЉЪБМфПЊеЙСЫЁАжњРЯжњВаЁЂЩчЧјЗўЮёЁЂЩњЬЌЛЗБЃЁЂЭјТчЮФУїЁБЫФИіжОдИЗўЮёЛюЖЏЃЈУПШЫжЛВЮМгвЛИіЛюЖЏЃЉЃЌОХФъМЖФГАрШЋАрЭЌбЇЖМВЮМгСЫжОдИЗўЮёЃЌАрГЄЮЊСЫНтжОдИЗўЮёЕФЧщПіЃЌЪеМЏећРэЪ§ОнКѓЃЌЛцжЦвдЯТВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓИУАрЕФШЫЪ§ЃЛ
ЃЈ2ЃЉЧыАбелЯпЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЧѓЩШаЮЭГМЦЭМжаЃЌЭјТчЮФУїВПЗжЖдгІЕФдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ4ЃЉаЁУїКЭаЁРіВЮМгСЫжОдИЗўЮёЛюЖЏЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЫћУЧВЮМгЭЌвЛЗўЮёЛюЖЏЕФИХТЪЃЎ
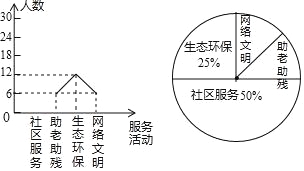
ЁОД№АИЁПЃЈ1ЃЉ48ЃЈ2ЃЉЭМаЮМћНтЮіЃЈ3ЃЉ45ЁуЃЈ4ЃЉ![]()
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнВЮМгЩњЬЌЛЗБЃЕФШЫЪ§вдМААйЗжБШЃЌМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЩчЧјЗўЮёЕФШЫЪ§ЃЌЛГіелЯпЭММДПЩЃЛ
ЃЈ3ЃЉИљОндВаФНЧ=360ЁуЁСАйЗжБШЃЌМЦЫуМДПЩЃЛ
ЃЈ4ЃЉгУСаБэЗЈМДПЩНтОіЮЪЬтЃЛ
ЪдЬтНтЮіЃКЃЈ1ЃЉИУАрШЋВПШЫЪ§ЃК12ЁТ25%=48ШЫЃЎ
ЃЈ2ЃЉ48ЁС50%=24ЃЌелЯпЭГМЦШчЭМЫљЪОЃК
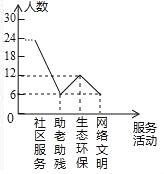
ЃЈ3ЃЉ![]() ЁС360Ёу=45ЁуЃЎ
ЁС360Ёу=45ЁуЃЎ
ЃЈ4ЃЉЗжБ№гУЁА1ЃЌ2ЃЌ3ЃЌ4ЁБДњБэЁАжњРЯжњВаЁЂЩчЧјЗўЮёЁЂЩњЬЌЛЗБЃЁЂЭјТчЮФУїЁБЫФИіЗўЮёЛюЖЏЃЌСаБэШчЯТЃК
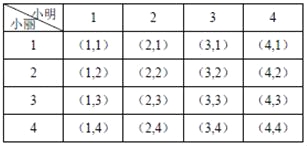
дђЫљгаПЩФмга16жжЃЌЦфжаЫћУЧВЮМгЭЌвЛЛюЖЏга4жжЃЌ
ЫљвдЫћУЧВЮМгЭЌвЛЗўЮёЛюЖЏЕФИХТЪP=![]() =
=![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіСуМўЕФаЮзДШчЭМЃЌАДЙцЖЈЁЯA= 90ЁуЃЌЁЯBЁЂЁЯC ЗжБ№ЪЧ 32ЁуКЭ 21ЁуЃЎФГМьбщЙЄШЫСПЕУЁЯBDC= 148ЁуЃЌОЭЖЯЖЈетИіСуМўВЛКЯИёЃЌЪдгУШ§НЧаЮЕФгаЙижЊЪЖЫЕУїСуМўВЛКЯИёЕФРэгЩЃЎ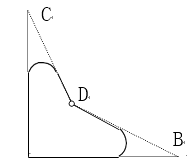
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОнЙњЭСзЪдДВПЪ§ОнЯдЪОЃЌЮвЙњЪЧШЋЧђЁАПЩШМБљЁБзЪдДДЂСПзюЖрЕФЙњМвжЎвЛЃЌКЃЁЂТНзмДЂСПдМЮЊ39000000000ЖжгЭЕБСПЃЌНЋ39000000000гУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈ ЃЉ
A.3.9ЁС1010
B.3.9ЁС109
C.0.39ЁС1011
D.39ЁС109
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫЕУїДњЪ§ЪН[ЃЈxЉyЃЉ2ЉЃЈx+yЃЉЃЈxЉyЃЉ]ЁТЃЈЉ2yЃЉ+yЕФжЕЃЌгыyЕФжЕЮоЙиЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
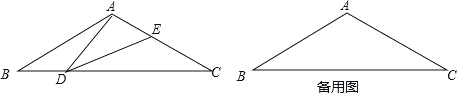
ЁОЬтФПЁПШчЭМЃЌдкЕШбќШ§НЧаЮABCжаЃЌЁЯBAC=120ЁуЃЌAB=AC=2ЃЌЕуDЪЧBCБпЩЯЕФвЛИіЖЏЕуЃЈВЛгыBЁЂCжиКЯЃЉЃЌдкACЩЯШЁвЛЕуEЃЌЪЙЁЯADE=30ЁуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABDЁзЁїDCEЃЛ
ЃЈ2ЃЉЩшBD=xЃЌAE=yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБЁїADEЪЧЕШбќШ§НЧаЮЪБЃЌЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШбќШ§НЧаЮгаСНЬѕБпЗжБ№ЪЧ3КЭ7ЃЌдђетИіШ§НЧаЮЕФжмГЄЪЧ_______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгЩЖрЯюЪНГЫЗЈЃКЃЈx+aЃЉЃЈx+bЃЉ=x2+ЃЈa+bЃЉx+abЃЌНЋИУЪНДггвЕНзѓЪЙгУЃЌМДПЩЕУЕНЁАЪЎзжЯрГЫЗЈЁБНјаавђЪНЗжНтЕФЙЋЪНЃКx2+ЃЈa+bЃЉx+ab=ЃЈx+aЃЉЃЈx+bЃЉ
ЪОР§ЃКЗжНтвђЪНЃКx2+5x+6=x2+ЃЈ2+3ЃЉx+2ЁС3=ЃЈx+2ЃЉЃЈx+3ЃЉ
ЃЈ1ЃЉГЂЪдЃКЗжНтвђЪНЃКx2+6x+8=ЃЈx+ЃЉЃЈx+ЃЉЃЛ
ЃЈ2ЃЉгІгУЃКЧыгУЩЯЪіЗНЗЈНтЗНГЬЃКx2Љ3xЉ4=0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋдАЦНУцЭМЩЯгавЛЬѕГЄ12cmЕФТЬЛЏДјЃЎШчЙћБШР§ГпЮЊ1ЃК2000ЃЌФЧУДетЬѕТЬЛЏДјЕФЪЕМЪГЄЖШЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§КЭаЮЪЧЪ§бЇЕФСНИіжївЊбаОПЖдЯѓЃЌЮвУЧОГЃдЫгУЪ§аЮНсКЯЁЂЪ§аЮзЊЛЏЕФЗНЗЈНтОівЛаЉЪ§бЇЮЪЬтЁЃЯТУцЮвУЧРДЬНОПЁАгЩЪ§ЫМаЮЃЌвдаЮжњЪ§ЁБЕФЗНЗЈдкНтОіДњЪ§ЮЪЬтжаЕФгІгУЃЎ
ЬНОПвЛЃКЧѓВЛЕШЪН![]() ЕФНтМЏ
ЕФНтМЏ
ЃЈ1ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
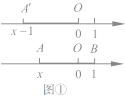
ШчЭМЂйЃЌдквдOЮЊдЕуЕФЪ§жсЩЯЃЌЩшЕуAЃЇЖдгІЕуЕФЪ§ЮЊ![]() ЃЌгЩОјЖджЕЕФЖЈвхПЩжЊЃЌЕуAЃЇгыOЕФОрРыЮЊ
ЃЌгЩОјЖджЕЕФЖЈвхПЩжЊЃЌЕуAЃЇгыOЕФОрРыЮЊ![]() ЃЌ
ЃЌ
ПЩМЧЮЊЃКAЃЇO=![]() ЁЃНЋЯпЖЮAЃЇOЯђгвЦНвЦвЛИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌЃЌДЫЪБЕуAЖдгІЕФЪ§ЮЊ
ЁЃНЋЯпЖЮAЃЇOЯђгвЦНвЦвЛИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌЃЌДЫЪБЕуAЖдгІЕФЪ§ЮЊ![]() ЃЌЕуBЕФЖдгІЪ§ЪЧ1ЃЌ
ЃЌЕуBЕФЖдгІЪ§ЪЧ1ЃЌ
вђЮЊAB= AЃЇOЃЌЫљвдAB=![]() ЁЃ
ЁЃ
вђДЫЃЌ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЪ§жсЩЯ
ЕФМИКЮвтвхПЩвдРэНтЮЊЪ§жсЩЯ![]() ЫљЖдгІЕФЕуAгы1ЫљЖдгІЕФЕуBжЎМфЕФОрРыABЁЃ
ЫљЖдгІЕФЕуAгы1ЫљЖдгІЕФЕуBжЎМфЕФОрРыABЁЃ
ЃЈ2ЃЉЧѓЗНГЬ![]() =2ЕФНт
=2ЕФНт
вђЮЊЪ§жсЩЯ3гы![]() ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЖМЮЊ2ЃЌЫљвдЗНГЬЕФНтЮЊ
ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЖМЮЊ2ЃЌЫљвдЗНГЬЕФНтЮЊ![]()
ЃЈ3ЃЉЧѓВЛЕШЪН![]() ЕФНтМЏ
ЕФНтМЏ
вђЮЊ![]() БэЪОЪ§жсЩЯ
БэЪОЪ§жсЩЯ![]() ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЃЌЫљвдЧѓВЛЕШЪННтМЏОЭзЊЛЏЮЊЧѓетИіОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§
ЫљЖдгІЕФЕугы1ЫљЖдгІЕФЕужЎМфЕФОрРыЃЌЫљвдЧѓВЛЕШЪННтМЏОЭзЊЛЏЮЊЧѓетИіОрРыаЁгк2ЕФЕуЫљЖдгІЕФЪ§![]() ЕФЗЖЮЇЁЃ
ЕФЗЖЮЇЁЃ
ЧыдкЭМЂкЕФЪ§жсЩЯБэЪО![]() ЕФНтМЏЃЌВЂаДГіетИіНтМЏ
ЕФНтМЏЃЌВЂаДГіетИіНтМЏ
![]()
ЬНОПЖўЃКЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ЃЈ1ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
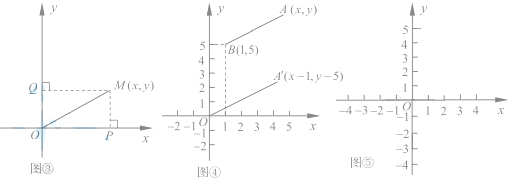
ШчЭМЂлЃЌдкжБНЧзјБъЯЕжаЃЌЩшЕуMЕФзјБъЮЊ![]() ЃЌЙ§MзїMPЁЭxжсгкPЃЌзїMQЁЭyжсгкQЃЌдђЕуPЕузјБъЃЈ
ЃЌЙ§MзїMPЁЭxжсгкPЃЌзїMQЁЭyжсгкQЃЌдђЕуPЕузјБъЃЈ![]() ЃЉЃЌQЕузјБъЃЈ
ЃЉЃЌQЕузјБъЃЈ![]() ЃЉЃЌ|OP|=
ЃЉЃЌ|OP|=![]() ЃЌ|OQ|=
ЃЌ|OQ|=![]() ЃЌ
ЃЌ
дкRtЁїOPMжаЃЌPMЃНOQЃНyЃЌдђ![]()
вђДЫ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуM
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуM![]() гыдЕуOЃЈ0,0ЃЉжЎМфЕФОрРыOM
гыдЕуOЃЈ0,0ЃЉжЎМфЕФОрРыOM
ЃЈ2ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ШчЭМЂмЃЌдкжБНЧзјБъЯЕжаЃЌЩшЕу AЃЇЕФзјБъЮЊ![]() ЃЌгЩЬНОПЃЈЖўЃЉЃЈ1ЃЉПЩжЊЃЌ
ЃЌгЩЬНОПЃЈЖўЃЉЃЈ1ЃЉПЩжЊЃЌ
AЃЇO=![]() ЃЌНЋЯпЖЮ AЃЇOЯШЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ5ИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌДЫЪБAЕФзјБъЮЊЃЈ
ЃЌНЋЯпЖЮ AЃЇOЯШЯђгвЦНвЦ1ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ5ИіЕЅЮЛЃЌЕУЕНЯпЖЮABЃЌДЫЪБAЕФзјБъЮЊЃЈ![]() ЃЉЃЌЕуBЕФзјБъЮЊЃЈ1,5ЃЉЁЃ
ЃЉЃЌЕуBЕФзјБъЮЊЃЈ1,5ЃЉЁЃ
вђЮЊAB= AЃЇOЃЌЫљвд AB=![]() ЃЌвђДЫ
ЃЌвђДЫ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ
ЕФМИКЮвтвхПЩвдРэНтЮЊЕуAЃЈ![]() ЃЉгыЕуBЃЈ1,5ЃЉжЎМфЕФОрРыЁЃ
ЃЉгыЕуBЃЈ1,5ЃЉжЎМфЕФОрРыЁЃ
ЃЈ3ЃЉЬНОП![]() ЕФМИКЮвтвх
ЕФМИКЮвтвх
ЧыЗТееЬНОПЖўЃЈ2ЃЉЕФЗНЗЈЃЌдкЭМЂнжаЛГіЭМаЮЃЌВЂаДГіЬНОПЙ§ГЬЁЃ
ЃЈ4ЃЉ![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЃК_________________________.
ЕФМИКЮвтвхПЩвдРэНтЮЊЃК_________________________.
ЭиеЙгІгУЃК
ЃЈ1ЃЉ![]() +
+![]() ЕФМИКЮвтвхПЩвдРэНтЮЊЃКЕуA
ЕФМИКЮвтвхПЩвдРэНтЮЊЃКЕуA![]() гыЕуE
гыЕуE![]() ЕФОрРыгыЕуAA
ЕФОрРыгыЕуAA![]() гыЕуF____________ЃЈЬюаДзјБъЃЉЕФОрРыжЎКЭЁЃ
гыЕуF____________ЃЈЬюаДзјБъЃЉЕФОрРыжЎКЭЁЃ
ЃЈ2ЃЉ![]() +
+![]() ЕФзюаЁжЕЮЊ____________(жБНгаДГіНсЙћ)
ЕФзюаЁжЕЮЊ____________(жБНгаДГіНсЙћ)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com