【题目】比﹣1小3的数是（ ）
A.4B.2C.﹣2D.﹣4
优学名师名题系列答案科目：初中数学 来源： 题型：
【题目】据国土资源部数据显示，我国是全球“可燃冰”资源储量最多的国家之一，海、陆总储量约为39000000000吨油当量，将39000000000用科学记数法表示为（ ）
A.3.9×1010
B.3.9×109
C.0.39×1011
D.39×109
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】由多项式乘法：（x+a）（x+b）=x2+（a+b）x+ab，将该式从右到左使用，即可得到“十字相乘法”进行因式分解的公式：x2+（a+b）x+ab=（x+a）（x+b）
示例：分解因式：x2+5x+6=x2+（2+3）x+2×3=（x+2）（x+3）
（1）尝试：分解因式：x2+6x+8=（x+）（x+）；
（2）应用：请用上述方法解方程：x2﹣3x﹣4=0．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店第一次用600元购进2B铅笔若干支，第二次又用600元购进该款铅笔，但这次每支的进价是第一次进价的 
倍，购进数量比第一次少了30支．
（1）求第一次每支铅笔的进价是多少元？
（2）若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元，问每支售价至少是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.过一点有且只有一条直线与已知直线平行
B.同旁内角互补
C.点到直线的距离就是这点到这条直线所作的垂线段
D.实数与数轴上的点一一对应
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题。下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．
探究一：求不等式
的解集
（1）探究
的几何意义
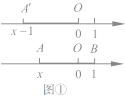
如图①，在以O为原点的数轴上，设点A＇对应点的数为
，由绝对值的定义可知，点A＇与O的距离为
，
可记为：A＇O=
。将线段A＇O向右平移一个单位，得到线段AB，，此时点A对应的数为
，点B的对应数是1，
因为AB= A＇O，所以AB=。
因此，的几何意义可以理解为数轴上
所对应的点A与1所对应的点B之间的距离AB。
（2）求方程=2的解
因为数轴上3与
所对应的点与1所对应的点之间的距离都为2，所以方程的解为
（3）求不等式
的解集
因为
表示数轴上
所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点所对应的数
的范围。
请在图②的数轴上表示的解集，并写出这个解集
探究二：探究
的几何意义
（1）探究
的几何意义
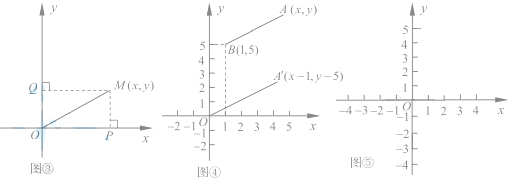
如图③，在直角坐标系中，设点M的坐标为
，过M作MP⊥x轴于P，作MQ⊥y轴于Q，则点P点坐标（
），Q点坐标（
），|OP|=
，|OQ|=
，
在Rt△OPM中，PM＝OQ＝y，则
因此
的几何意义可以理解为点M
与原点O（0,0）之间的距离OM
（2）探究
的几何意义
如图④，在直角坐标系中，设点 A＇的坐标为
，由探究（二）（1）可知，
A＇O=
，将线段 A＇O先向右平移1个单位，再向上平移5个单位，得到线段AB，此时A的坐标为（
），点B的坐标为（1,5）。
因为AB= A＇O，所以 AB=，因此的几何意义可以理解为点A（
）与点B（1,5）之间的距离。
（3）探究
的几何意义
请仿照探究二（2）的方法，在图⑤中画出图形，并写出探究过程。
（4）
的几何意义可以理解为：_________________________.
拓展应用：
（1）
+
的几何意义可以理解为：点A
与点E
的距离与点AA
与点F____________（填写坐标）的距离之和。
（2）
+
的最小值为____________(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
