
【题目】在△ABC中,AB=AC.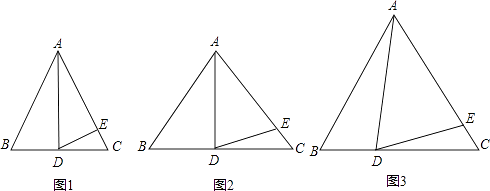
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.
【答案】
(1)15°
(2)20°
(3)∠EDC= ![]() ∠BAD
∠BAD
(4)解:仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC.
故分别填15°,20°,∠EDC= ![]() ∠BAD
∠BAD
【解析】(1)根据等腰三角形的性质三线合一和∠BAD=30°,得到△ABC是等边三角形,由AD=AE和三角形的一个外角等于和它不相邻的两个内角之和
,求出∠EDC的度数;(2)由∠BAD=40°,AD是BC上的高,AD=AE,根据三角形内角和定理和三线合一,求出∠EDC的度数;(3)根据等腰三角形的性质和三角形内角和定理,得出结论∠EDC=![]() ∠BAD.
∠BAD.


科目:初中数学 来源: 题型:
【题目】由多项式乘法:(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左使用,即可得到“十字相乘法”进行因式分解的公式:x2+(a+b)x+ab=(x+a)(x+b)
示例:分解因式:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3)
(1)尝试:分解因式:x2+6x+8=(x+)(x+);
(2)应用:请用上述方法解方程:x2﹣3x﹣4=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行
B.同旁内角互补
C.点到直线的距离就是这点到这条直线所作的垂线段
D.实数与数轴上的点一一对应
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题。下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式![]() 的解集
的解集
(1)探究![]() 的几何意义
的几何意义
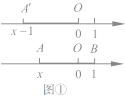
如图①,在以O为原点的数轴上,设点A'对应点的数为![]() ,由绝对值的定义可知,点A'与O的距离为
,由绝对值的定义可知,点A'与O的距离为![]() ,
,
可记为:A'O=![]() 。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为
。将线段A'O向右平移一个单位,得到线段AB,,此时点A对应的数为![]() ,点B的对应数是1,
,点B的对应数是1,
因为AB= A'O,所以AB=![]() 。
。
因此,![]() 的几何意义可以理解为数轴上
的几何意义可以理解为数轴上![]() 所对应的点A与1所对应的点B之间的距离AB。
所对应的点A与1所对应的点B之间的距离AB。
(2)求方程![]() =2的解
=2的解
因为数轴上3与![]() 所对应的点与1所对应的点之间的距离都为2,所以方程的解为
所对应的点与1所对应的点之间的距离都为2,所以方程的解为![]()
(3)求不等式![]() 的解集
的解集
因为![]() 表示数轴上
表示数轴上![]() 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数
所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点所对应的数![]() 的范围。
的范围。
请在图②的数轴上表示![]() 的解集,并写出这个解集
的解集,并写出这个解集
![]()
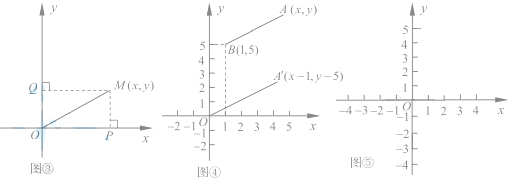
探究二:探究![]() 的几何意义
的几何意义
(1)探究![]() 的几何意义
的几何意义
如图③,在直角坐标系中,设点M的坐标为![]() ,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(
,过M作MP⊥x轴于P,作MQ⊥y轴于Q,则点P点坐标(![]() ),Q点坐标(
),Q点坐标(![]() ),|OP|=
),|OP|=![]() ,|OQ|=
,|OQ|=![]() ,
,
在Rt△OPM中,PM=OQ=y,则![]()
因此![]() 的几何意义可以理解为点M
的几何意义可以理解为点M![]() 与原点O(0,0)之间的距离OM
与原点O(0,0)之间的距离OM
(2)探究![]() 的几何意义
的几何意义
如图④,在直角坐标系中,设点 A'的坐标为![]() ,由探究(二)(1)可知,
,由探究(二)(1)可知,
A'O=![]() ,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(
,将线段 A'O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时A的坐标为(![]() ),点B的坐标为(1,5)。
),点B的坐标为(1,5)。
因为AB= A'O,所以 AB=![]() ,因此
,因此![]() 的几何意义可以理解为点A(
的几何意义可以理解为点A(![]() )与点B(1,5)之间的距离。
)与点B(1,5)之间的距离。
(3)探究![]() 的几何意义
的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程。
(4)![]() 的几何意义可以理解为:_________________________.
的几何意义可以理解为:_________________________.
拓展应用:
(1)![]() +
+![]() 的几何意义可以理解为:点A
的几何意义可以理解为:点A![]() 与点E
与点E![]() 的距离与点AA
的距离与点AA![]() 与点F____________(填写坐标)的距离之和。
与点F____________(填写坐标)的距离之和。
(2)![]() +
+![]() 的最小值为____________(直接写出结果)
的最小值为____________(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若定义:f(a,b)=(-a,b),g(m,n)=(m,-n),例如f(1,2)=(-1,2),g(-4,-5)=(-4,5),则g(f(3,-4))的值为( )
A.(3,-4)B.(-3,4)C.(3,4)D.(-3,-4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图4所示.
(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三边作三角形,用到的基本作图是( )
A. 作一个角等于已知角 B. 平分一个已知角
C. 在射线上截取一线段等于已知线段 D. 作一条直线的垂线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A,B,C三点坐标分别是(0,0),(4,0),(3,2),以A,B,C三点
为顶点画平行四边形,则第四个顶点不可能在( ).
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com