
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
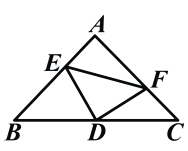
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
【答案】(1)BE=12,CF=5;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)先根据二次根式的非负性求出m=2,再由非负数的性质求出a、b的值,进而得到BE及CF的长;
(2)延长ED到P,使DP=DE,连接FP,CP,利用SAS得到三角形BED与三角形CPD全等,利用全等三角形对应边相等得到BE=CP,再利用SAS得到△EDF和△PDF全等,利用全等三角形对应边相等得到EF=FP,利用等角的余角相等得到∠FCP为直角,在直角三角形FCP中,利用勾股定理列出关系式,等量代换即可得证;
(3)连接AD,由AB=AC,且D为BC的中点,利用三线合一得到AD垂直于BC,AD为角平分线,再由三角形ABC为等腰直角三角形,得到一对角相等,利用同角的余角相等得到一对角相等,再由AD=CD,利用ASA得到三角形AED与三角形CFD全等,利用全等三角形对应边相等得到AE=CF=5,DE=DF,由AE+EB求出AB的长,即为AC的长,再由AC-CF求出AF的长,在直角三角形AEF中,利用勾股定理求出EF的长,再根据三角形DEF为等腰直角三角形求出DE与DF的长,即可确定出三角形DEF的面积.
试题解析:(1)由题意得![]() ,
,
解得m=2,
则![]() +|b-5|=0,
+|b-5|=0,
所以a-12=0,b-5=0,
a=12,b=5,
即BE=12,CF=5;
(2)延长ED到P,使DP=DE,连接FP,CP,
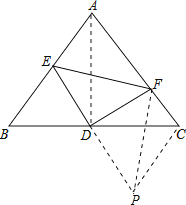
在△BED和△CPD中,
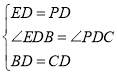 ,
,
∴△BED≌△CPD(SAS),
∴BE=CP,∠B=∠CDP,
在△EDF和△PDF中,
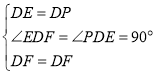 ,
,
∴△EDF≌△PDF(SAS),
∴EF=FP,
∵∠B=∠DCP,∠A=90°,
∴∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°,
在Rt△FCP中,根据勾股定理得:CF2+CP2=PF2,
∵BE=CP,PF=EF,
∴BE2+CF2=EF2;
(3)连接AD,
∵△ABC为等腰直角三角形,D为BC的中点,
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∵ED⊥FD,
∴∠EDA+∠ADF=90°,∠ADF+∠FDC=90°,
∴∠EDA=∠FDC,
在△AED和△CFD中,
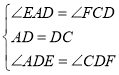 ,
,
∴△AED≌△CFD(ASA),
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴AB=AE+EB=5+12=17,
∴AF=AC-FC=AB-CF=17-5=12,
在Rt△EAF中,根据勾股定理得:EF=![]() =13,
=13,
设DE=DF=x,
根据勾股定理得:x2+x2=132,
解得:x=![]() ,即DE=DF=
,即DE=DF=![]() ,
,
则S△DEF=![]() DEDF=
DEDF=![]() ×
×![]() ×
×![]() =
=![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】电影《流浪地球》中,人类计划带着地球一起逃到距地球4光年的半人马星座比邻星.已知光年是天文学中的距离单位,1光年大约是95000亿千米,则4光年约为( )
A. 9.5×104亿千米B. 95×104亿千米
C. 3.8×105亿千米D. 3.8×104亿千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是
A.x1=1,x2=3B.x1=1,x2=﹣3C.x1=﹣1,x2=3D.x1=﹣1,x2=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB=,AB∶BC=2∶3,求圆的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=3x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )
A.y=3x2+2
B.y=(3x+2)2
C.y=3(x+2)2
D.y=3(x﹣2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在暑假到来之前,某机构向八年级学生推荐了A,B,C三条游学线路,现对全级学生喜欢哪一条游学线路作调查,以决定最终的游学线路,下面的统计量中最值得关注的是( )
A. 方差 B. 平均数 C. 中位数 D. 众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:“半角问题”:
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究此“半角问题”的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;(直接写结论,不需证明)
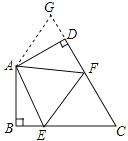
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=![]() ∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形,那么原四边形ABCD为( )
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com