
【题目】问题背景:“半角问题”:
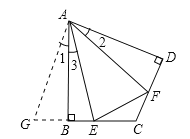
(1)如图:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究此“半角问题”的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;(直接写结论,不需证明)
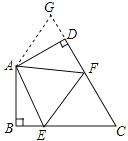
探索延伸:当聪明的你遇到下面的问题该如何解决呢?
(2)若将(1)中“∠BAD=120°,∠EAF=60°”换为∠EAF=![]() ∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD.其它条件不变。如图1,试问线段EF、BE、FD具有怎样的数量关系,并证明.
(3)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
∠BAD,请直接写出线段EF、BE、FD它们之间的数量关系.(不需要证明)
(4)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.
∠BAD,试问线段EF、BE、FD具有怎样的数量关系,并证明.

【答案】见解析
【解析】试题分析:(1)根据提示步骤及结论直接得出EF=BE+DF;
(2)可通过构建全等三角形来实现线段间的转换.延长EB到G,使BG=DF,连接AG.目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE,那么这样EF=BE+DF了,于是证明两组三角形全等就是解题的关键.三角形ABE和AEF中,只有一条公共边AE,我们就要通过其他的全等三角形来实现,在三角形ABG和AFD中,已知了一组直角,BG=DF,AB=AD,因此两三角形全等,那么AG=AF,∠1=∠2,那么∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.
(3)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.
(4)按照之前的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE-BG=BE-DF.所以(1)的结论在(3)的条件下是不成立的.
试题解析:
(1)EF=BE+FD.
(2)如图所示:延长EB到G,使BG=DF,连接AG.
∵在△ABG与△ADF中,
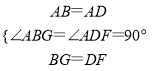
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAE=∠EAF.
又AE=AE,
易证△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(3)EF=BE+FD;
(4)结论EF=BE+FD不成立,应当是EF=BE-FD.
证明:在BE上截取BG,使BG=DF,连接AG,如图所示:
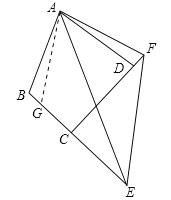
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵在△ABG与△ADF中,
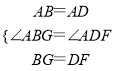
∴△ABG≌△ADF(SAS).
∴∠BAG=∠DAF,AG=AF.
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
易证△AEG≌△AEF.
∴EG=EF,
∵EG=BE-BG,
∴EF=BE-FD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
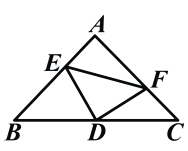
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC,分别以AB、AC边作图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,下列结论①△AEC≌△ABF,②EC=FB,③EC⊥FB,④MA平分∠EMF中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.有一个角是直角的平行四边形是正方形
B.有一组邻边相等的矩形是正方形
C.对角线相等且互相垂直的四边形是正方形
D.四条边都相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据某省统计局发布,2017年该省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年该省有效发明专利为a万件,则2018年该省有效发明专利为( )
A. (1+2×22.1%)a B. (1+22.1%)×2a
C. (1+22.1%)2a D. 22.1%×2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.三条边相等的四边形是菱形
B.对角线相等的平行四边形是矩形
C.对角线互相垂直且相等的四边形是正方形
D.一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com