【题目】据某省统计局发布，2017年该省有效发明专利数比2016年增长22.1%．假定2018年的年增长率保持不变，2016年该省有效发明专利为a万件，则2018年该省有效发明专利为（ ）
A. （1+2×22.1%）a B. （1+22.1%）×2a
C. （1+22.1%）2a D. 22.1%×2a
科目：初中数学 来源： 题型：
【题目】我们知道方程x2+2x﹣3=0的解是x1=1，x2=﹣3，现给出另一个方程（2x+3）2+2（2x+3）﹣3=0，它的解是
A.x1=1，x2=3B.x1=1，x2=﹣3C.x1=﹣1，x2=3D.x1=﹣1，x2=﹣3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在暑假到来之前，某机构向八年级学生推荐了A，B，C三条游学线路，现对全级学生喜欢哪一条游学线路作调查，以决定最终的游学线路，下面的统计量中最值得关注的是（ ）
A. 方差 B. 平均数 C. 中位数 D. 众数
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题背景：“半角问题”：
（1）如图：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段EF，BE，FD之间的数量关系．
小明同学探究此“半角问题”的方法是：延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；（直接写结论，不需证明）
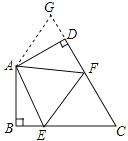
探索延伸：当聪明的你遇到下面的问题该如何解决呢？
（2）若将（1）中“∠BAD=120°，∠EAF=60°”换为∠EAF=
∠BAD．其它条件不变。如图1，试问线段EF、BE、FD具有怎样的数量关系，并证明．
（3）如图2，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=
∠BAD，请直接写出线段EF、BE、FD它们之间的数量关系．（不需要证明）
（4）如图3，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=
∠BAD，试问线段EF、BE、FD具有怎样的数量关系，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(2016山东潍坊第18题)在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的坐标是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
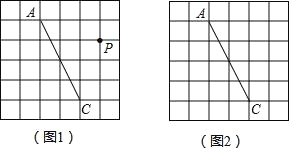
【题目】图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．
（1）如图1，点P在小正方形的顶点上，在图1中作出点P关于直线AC的对称点Q，连接AQ、QC、CP、PA，并直接写出四边形AQCP的周长；
（2）在图2中画出一个以线段AC为对角线、面积为6的矩形ABCD，且点B和点D均在小正方形的顶点上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形，那么原四边形ABCD为（ ）
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
