
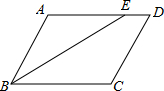
 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )| A. | ∠C=120° | B. | AE=6cm | C. | AD=8cm | D. | ∠BED=140° |
分析 由?ABCD中,BC=8cm,CD=6cm,∠D=60°,根据平行四边形的性质,可求得∠C=120°;又由BE平分∠ABC,易求得∠AEB=∠ABE=∠EBC=30°,∠BED=150°,继而可求得AE=AB=CD=6cm,ED=AD-AE=2.
解答 解:∵四边形ABCD是平行四边形,∠D=50°,
∴AD∥BC,AD=BC=8cm,AB=CD=6cm,∠ABC=∠D=60°,
∴∠C=180°-∠D=120°,故A正确;
∵BE平分∠ABC,
∴∠ABE=∠EBC=$\frac{1}{2}$∠ABC=30°,
∴∠AEB=∠EBC=30°,
∴∠BED=180°-∠AEB=150°,故D错误;
∴∠AEB=∠ABE,
∴AE=AB=6cm,故B正确;
AD=BC=8cm,故C正确.
故选D.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.此题难度不大,注意数形结合思想的应用.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
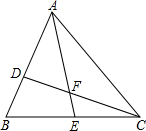 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
斐波那契(约1170-1250)是意大利数学家,他研究了一列数, 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到 的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的 瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质, 在实际生活中也有广泛的应用. 斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$ 表示(其中n≥1),这是用无理数表示有理数的一个范例. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com