
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 设树苗总数为x棵,根据各班的树苗数都相等,可得出第一班和第二班领取的树苗数相等,由此可得出方程.
解答 解:设树苗总数是x棵,班级数是y个,根据题意列出的方程或方程组有(1)100+$\frac{1}{10}$(x-100)=200+$\frac{1}{10}${x-[100+$\frac{1}{10}$(x-100)]-200}
(2)100y=100(y-1)+$\frac{1}{9}$×100y
(3)$\left\{\begin{array}{l}{[100+\frac{1}{10}(x-100)]y=x}\\{100{y}^{2}=x}\end{array}$
(4)(x-100)[$\frac{1}{10}-(1-\frac{1}{10})×\frac{1}{10}]=(200-100)-200×\frac{1}{10}$=(200-100)-200×$\frac{1}{10}$.
故选D.
点评 本题考查了一元一次方程的应用,解答本题的关键是得出各班的树苗数都相等,这个等量关系,因为第一班,第二班领取数量好表示,所以我们就选取这两班建立等量关系.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
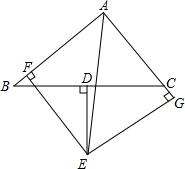 如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,
如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
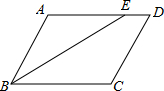 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )| A. | ∠C=120° | B. | AE=6cm | C. | AD=8cm | D. | ∠BED=140° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com