
【题目】如图,点D,E分别在线段AB, AC上,CD与BE相交于O点,已知AD=AE,现添加以下哪个条件仍不能判定△ABE≌△ACD( )

A. BD= CEB. ∠B=∠CC. BE=CDD. AB=AC
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是宽为a,长为b的长方形。用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形。
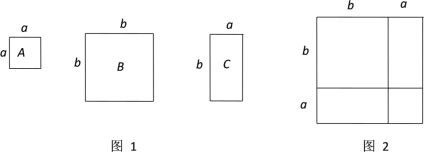
(1)请用两种不同的方式表示图2大正方形的面积。
方式1: ;
方式2: .
(2)观察图2,请你写出下列三个代数式:![]() ,
,![]() ,
,![]() 之间的等量关系。
之间的等量关系。
(3)类似地,请你用图1中的三种纸片拼一个图形验证:
![]()
(4)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,求
,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )
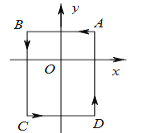
A. (-1,0)B. (1,2)C. (1,-1)D. (0,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC平分∠PAQ,点B、B′分别在边AP、AQ上,如果添加一个条件,即可推出AB=AB′,下列条件中无法推出AB=AB′的是( )
A. BB′⊥AC B. BC=B′C C. ∠ACB=∠ACB′ D. ∠ABC=∠AB′C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(1,0),B(2,﹣3),C(4,﹣2).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1向左平移3个单位长度后得到的△A2B2C2;
(3)如果AC上有一点P(m,n)经过上述两次变换,那么对应A2C2上的点P2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
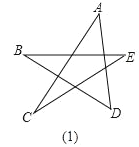
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
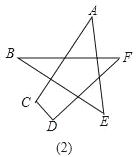
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
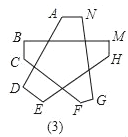
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠2,∠C=∠E, AE=AC,
(1)求证: △ABC≌△ADE;
(2) 求证:∠2=∠3;
(3)当∠2=90°时,判断△ABD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点(-1,0),对称轴为:直线x=1,则下列结论中正确的是:( )
A.a>0
B.当x>1时,y随x的增大而增大
C.![]() <0
<0
D.x=3是一元二次方程ax2+bx+c=0(a≠0)的一个根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com