

分析 分两种情况进行讨论:①当P在A、E之间时,∠CPD=α-β;②当P在B、E之间时,∠CPD=α+β;先过点P作PF∥MN,再根据平行线的性质,得出∠BCP=∠FPC=α,∠MDP=∠FPD=β,最后根据角的和差关系得出结论.
解答 解:(1)如图,①当P在A、E之间时,∠CPD=α-β;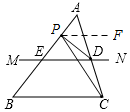
如图,②当P在B、E之间时,∠CPD=α+β;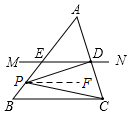
(2)选择①当P在A、E之间时,∠CPD=α-β;
证明:过点P作PF∥MN,则PF∥BC,
∴∠BCP=∠FPC=α,∠MDP=∠FPD=β,
∴∠CPD=∠FPC-∠FPD=∠BCP-∠MDP=α-β;
选择②当P在B、E之间时,∠CPD=α+β;
过点P作PF∥MN,则PF∥BC,
∴∠BCP=∠FPC=α,∠MDP=∠FPD=β,
∴∠CPD=∠FPC+∠FPD=∠BCP+∠MDP=α+β.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线,构造平行线,利用两直线平行,内错角相等进行证明.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
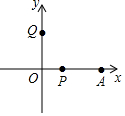 如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t;
如图,在平面直角坐标系中有一点A,OA=16,动点P从A开始以每秒2个单位的速度向x轴负半轴运动,动点Q从0开始以每秒1个单位的速度向y轴正半轴运动,P,Q同时出发,设时间为t;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com